Em cada item abaixo, determine os valores reais de que satisfazem as inequações.
c)
Passo 1
Eaee!! Tudo bem? Veja bem, irei te ajudar com essa resolução hoje. Daqui você vai sair sabendo tudo sobre inequações.
A gente quer saber quais são os intervalos reais de para satisfazer a inequação:
Para resolver essa questão o melhor a se fazer é reorganiza-la para que possamos analisarmos duas equações distintas.
Depois disso iremos analisar os sinais das duas equações, e assim poderemos obter o intervalo necessário em que ambas satisfazem as mesmas condições.
Passo 2
Manipulando a inequação, teremos:
Subtraindo em ambos os lados:
Agora vamos realizar a analise dos sinais individuais de ambas as funções, e saberemos os intervalos em que cada uma é positiva e negativa, com isso saberemos o intervalo em que a divisão delas será positiva ou negativa.
Passo 3
Primeiro vamos obter o gráfico da função por meio do GeoGebra:
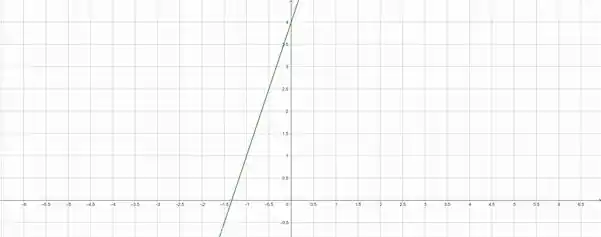
Então o nosso gráfico se divide em:
Para valores:
A função é positiva, para valores:
A função é negativa.
Vamos fazer a mesma analise para a outra equação. Primeiro o gráfico:
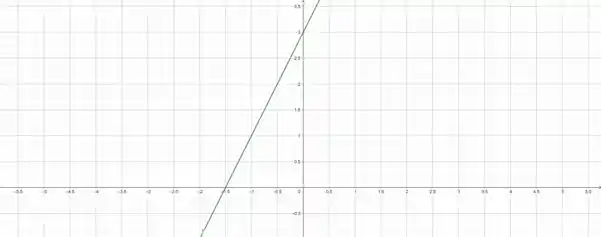
A divisão é a seguinte:
Para valores:
Nosso gráfico é positivo. Para valores:
Temos que nossa função é negativa.
Agora a gente vai analisar a operação de divisão.
Passo 4
Para que uma divisão seja positiva, que é que a gente busca, precisamos que ambos os valores sejam do mesmo sinal, isso é, ambas as funções precisam ser positivas, ou ambas precisam ser negativas.
Visualizando ambas as equações no gráfico:
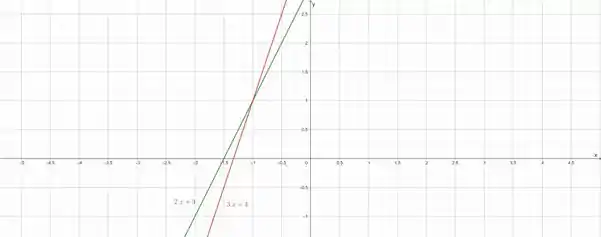
Vejamos que ambas serão negativas quando:
E ambas serão positivas quando:
Então, nosso intervalo resposta é: