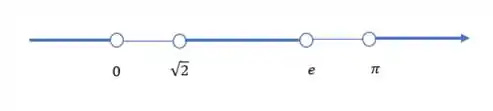
Reescrever os conjuntos abaixo usando a notação de intervalo e, a seguir, representá-los graficamente
Passo 1
E aí pessoal, tudo bem? O problema nos deu esse conjunto aqui
E pediu para reescrevermos usando a notação de intervalo e também para representar graficamente
Mas você lembra como fazer isso?
Então vem comigo! Primeiro precisamos verificar se o conjunto é aberto ou fechado. Se ele for aberto , em cima do número que representa esse extremo a bolinha não estará pintada, e isso nos diz que esse número não pertence ao nosso conjunto de interesse!![]()
Já quando for fechado , a bolinha estará pintada e isso significa que esse extremo está contido no nosso conjunto!

Então taí nossa representação gráfica! E quanto à representação de conjuntos? Bom, temos um extremo aberto quando usamos parênteses ou quando temos colchetes para fora . O extremo será fechado quando os colchetes estiverem para dentro, assim . Podemos usar alguma combinação desses símbolos, viu? Em cada ponta do intervalo podemos ter tanto aberto quanto fechado!

Beleza? Então bora colocar a mão na massa! Ah! Lembrando que quando temos , isso significa que nesse extremo o intervalo e aberto, ok?
Mas relaxa, vou fazer passo a passo com você!
Passo 2
Nosso conjunto é:
Temos que o intervalo pertence aos reais (então temos qualquer número, podemos usar a reta normal que usamos). Temos que precisa ser menor do que , ou estar entre (sem incluir) e . E ainda por cima pode ser maior do que !
Mas tem como isso acontecer simultaneamente?

Não tem! Então vamos separar nosso intervalo em três! E tá tudo bem fazer isso viu? A diferença que é que você vai escrever um entre os intervalos!
Tranquilo até aqui?

Para a primeira parte
Temos um limite superior para , que é o (sem incluir, então intervalo aberto), mas não inferior (intervalo também aberto). Assim nosso intervalo aqui fica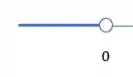
E a segunda parte temos como limite inferior o (sem incluir) e limite superior (sem incluir também). Então temos que os dois extremos são abertos

E a terceira parte temos que . Então temos um limite inferior que é (aberto pois não inclui) e não temos limite superior (que é , então aberto de novo)
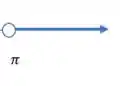
Tranquilo? Agora #partiu agrupar!
Passo 3
Agora agrupando essas três partes temos nosso conjunto completo
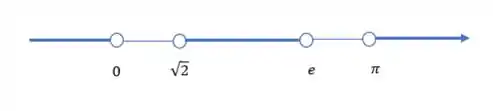
E é isso!
Espero ter ajudado! Vamos para a próxima?
Resposta