Dados os conjuntos e , efetue as operações pedidas e dê as respostas na notação de intervalo.
Passo 1
Primeiramente, vamos dar uma olhada em nossos dois intervalos, para ficar mais claro:
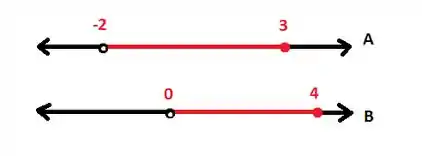
Vamos começar com a letra
Essa operação significa que vamos unir os dois intervalos, que graficamente seria o seguinte:
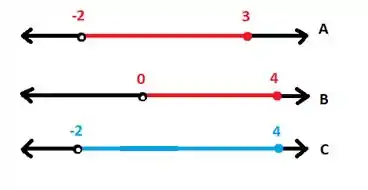
Perceba que a bolinha aberta some na união!!! Então o intervalo da união é:
Passo 2
A próxima letra pede:
Agora, não vamos unir os termos, vamos ver quais termos estão nos dois intervalos ao mesmo tempo! Olha o desenho:
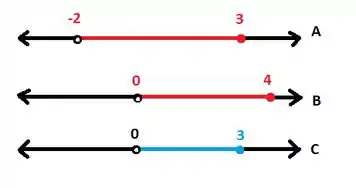
Agora é só escrever como intervalo:
Passo 3
Dá uma olhada nessa aqui:
Agora nós precisamos pegar o intervalo e tirar todos os elementos que estão em . Novamente, olhe o desenho (desenhos são as melhores técnicas para esse tipo de questão):
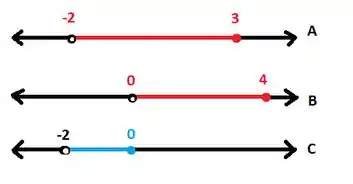
Agora é só escrever na notação de intervalo:
Passo 4
Olhaaaaaa, já estamos na última! Você tá indo bem, só mais uma, vem:
Então, a agora é justamente o contrário: vamos pegar o conjunto e tirar todos os elementos que estão no conjunto também. Olha o desenho de como fica:
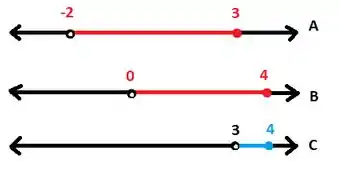
Perceba que temos uma bolinha aberta agora no , isso aconteceu porque estava no intervalo e no , portanto tivemos que tirá-lo dessa brincadeira! Agora escrevendo com a notação de intervalo:
FIMMM!