UFSCAR – Cálculo I – Listas - Teste 9 – Lista de Estudos Cálculo 1 - UFSCAR – Lista 1 – Versão 2 Questão 2d
Demonstre as seguintes propriedades:
d) ( é uma constante).
Passo 1
Eaee!!! Belezinha? Bom... a questão nos dá uma inequação e pede para demonstrarmos a propriedade envolvida naquela afirmação.
Bom, para esse caso, uma forma de demonstrar é estudando o sinal da função, ou seja, como ela se comporta em um intervalo.
Vamos devagarinho juntos para entendermos melhor 😉
Passo 2
Bom... seja . Graficamente temos:
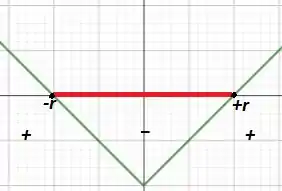
Bom, observando a expressão e o gráfico, vemos que será atendido ao mesmo tempo em que a expressão .
Dessa forma, observamos que o intervalo válido de resposta ocorre quando .
Entendeu direitinho? Responde aee ;)
Resposta
A resposta é dada por uma demonstração
Exercícios de Livros Relacionados
Expresse cada um dos conjuntos abaixo em notação de intervalo. x ∈ R | x1
Determine r0 de modo que 4 - r , 4 + r ⊂ 2,5 .(Lembre-se: A ⊂ B ↔ A é subconjunto de B .)
Expresse cada um dos conjuntos abaixo em notação de intervalo. x ∈ R | 3 x + 1x 3
Expresse cada um dos conjuntos abaixo em notação de intervalo. x ∈ R | 2 x - 3 ≤ 1
Expresse cada um dos conjuntos abaixo em notação de intervalo. x ∈ R |4 x - 36 x + 2