Sejam os intervalos reais é correto afirmar que:
Passo 1
Ok, dá pra ver que tem muita conta pra fazer, mas vamos nos adiantar logo em algumas coisas.
Guarda isso aí!
Falta só mais umazinha:
Passo 2
Agora que já fizemos nosso esboço, vamos atacar as alternativas!
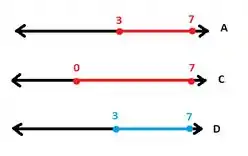
Olha como fica o desenho:
Lembrando que a primeira reta é e . Escrevendo em notação de intervalo:
Lembrando também que
Passo 3
Próxima alternativa:
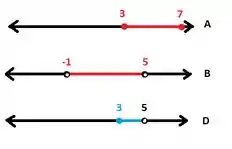
Olhe só o desenho de como o lado esquerdo fica:
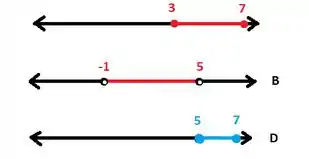
Lembrando que a primeira reta representa e . Escrevendo em forma de intervalo:
Agora vamos ver o desenho de :
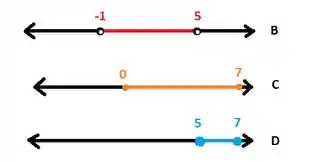
Perceba que são iguais, ou seja, essa está correta!!!
Passo 4
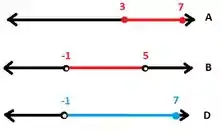
Olha só o desenho de como fica isso (lembrando que ):
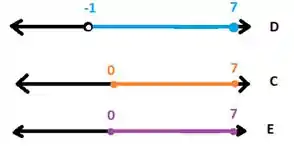
Passando isso pra notação de intervalo:
Logo, essa afirmação não é verdade.
Passo 5
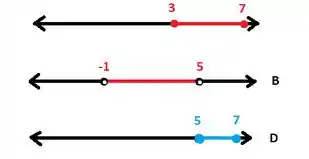
Saca só como fica o desenho dessa parada (lembrando que ):
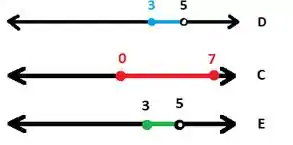
Escrevendo isso na notação de intervalo:
Portanto, esta não está certa.
Passo 6
Olha essa agora:
Se liga como fica o desenho (lembrando que ):
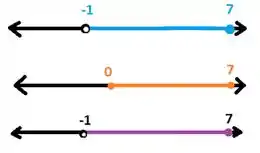
Passando isso pra notação de intervalo, ficamos com:
Lembrando que
Resposta
Letra