- Qual dos conjuntos abaixo é o domínio de ?
Passo 1
Oi, galerinha! Tudo bom? Aqui precisamos achar o domínio da função e para isso temos que lembrar qual a restrição das funções quadradicas e frações.
Para quem não lembra, as restrições são:
- o argumento de toda raiz par deve ser maior ou igual a zero.
- o denominador não pode ser zero.
Em outras palavras, temos que
E
Agora vamos analisar quais valores possíveis de .
Passo 2
Galerinha, vamos começar pela restrição da fração,
Ou seja, para saber o nosso domínio, vamos encontrar quais pontos que não pode ser. Para isso, temos que resolver a seguinte equação de segundo grau,
Aplicando Bhaskara, ficamos com
Logo,
Ou seja, o domínio não está definido em e .
Agora vamos para a nossa próxima restrição!
Passo 3
Vamos analisar,
Para descobrirmos qual intervalo que essa divisão será positiva, temos que analisar as partes (numerador e denominador) em separado e depois fazer um estudo do sinal.
Começando por,
Como, temos que , a nossa parábola é para cima. Logo, entre e .
Para a parte,
Já vimos que as raízes são e . E como , aqui a parábola também é para cima. Logo, entre e .
Vamos organizar os dados!
Passo 4
Organizando os dados numa tabela, temos a seguinte analise de sinal
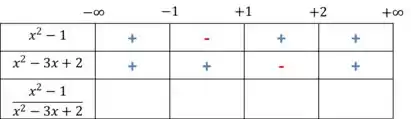
Jutando os dados,
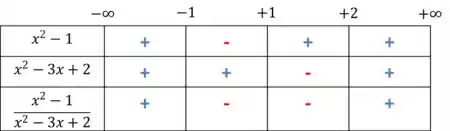
Ou seja, a função é negativa entre e . Logo ela não pode existir nesse intervalo.
Deste modo, o domínio da função será . Lembrando que ela pode existir em , mas não pode existir em (restrição do Passo 2).