UTFPR, Sem Campus, Cálculo Diferencial e Integral 2, Listas de Cáclulo 2 - Profº Félix Gómez - Primeira Lista, Questão 1.4a
Verificar quais dos seguintes conjuntos são conexos
Passo 1
Fala aí gente, tudo na paz com vocês?
Então, nessa questão recebemos o seguinte conjunto:
Ou seja, é um conjunto cujos pontos são definidos pela equação:
Precisamos verificar se esse conjunto é conexo.
Um conjunto conexo é aquele que não pode ser separado em dois conjuntos abertos disjuntos, ou seja, que não tem intersecção. Isso significa que o conjunto não pode ser separado em pedações desconectados.
Pra verificarmos isso, tem um bizu muito legal. Vamos desenhar a região no plano e verificar se para quaisquer dois pontos escolhidos conseguimos traçar um caminho entre eles que esteja todo contido dentro da região. Se isso acontecer, o conjunto é conexo, beleza?
Vamo nessa!
Passo 2
Vimos que o conjunto é definido por:
Vamos tentar deixar essa equação com a cara de alguma região que nós conhecemos.
Essa equação nos lembra a equação da região interna de uma elipse:
No nosso caso, a elipse está em pé, o eixo maior vale:
E o menor:
Assim, podemos esboçar a região como:
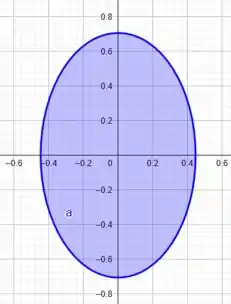
Perfeito!
Passo 3
Agora que já esboçamos a nossa região, vamos pensar sobre aquilo que comentamos no passo . Existe algum par de pontos que não seja possível traçar um caminho dentro da nossa região?
Não né?! A região interna da elipse não tem nenhum pedaço descontectado.
Logo, concluímos que o conjunto é um conjunto conexo.
E aí, curtiram? Até a próxima 😊
Resposta
Conexo.