UTFPR, Sem Campus, Cálculo Diferencial e Integral 2, Listas de Cáclulo 2 - Profº Félix Gómez - Primeira Lista, Questão 1.3e
Identificar as afirmações verdadeiras
O conjunto
é conexo.
Passo 1
Fala aí pessoal, tudo bem?
Nessa questão precisamos avaliar se o conjunto:
é, ou não, um conjunto conexo.
Pra começar, vocês lembram o que é um conjunto conexo?
Um conjunto conexo é aquele que não pode ser separado em dois conjuntos abertos disjuntos, ou seja, que não tem intersecção.
Por exemplo, o conjunto:
Conseguimos separá-lo em dois conjuntos abertos?! Poderíamos tentar fazer:
onde .
Tem um jeito bem bizurado de verificar se um conjunto é conexo ou não. Após desenhar a sua representação no espaço, verificamos se para quaisquer dois pontos escolhidos nessa região é possível traçar um caminho que pertença totalmente à região.
Então, vamos primeiro desenhar o conjunto para depois analisar o caminho.
Passo 2
Bom, temos que o conjunto é definido pela equação:
Assim, vem:
Ou seja, temos a região limitada pelas retas:
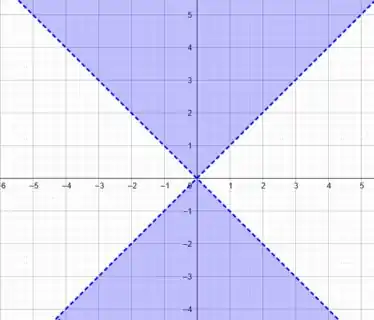
Massa!
Passo 3
Agora vamos pensar se conseguimos traçar um caminho entre quaisquer dois pontos.
Se tomarmos um ponto acima do eixo e outro abaixo do eixo , ficamos numa situação meio complicada galera.
Como o ponto não pertence a esse conjunto, não conseguimos traçar um caminho que ligue os dois pontos e ainda esteja dentro da nossa região.
Portanto, o conjunto é desconexo.
Prontinho, tchau tchau 😊
Resposta
Falso.