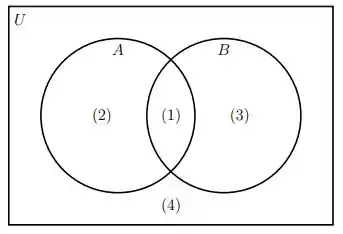
NO diagrama de Venn-Euler abaixo, cada região foi denominada com um número entre parênteses. Indicar as regiões que determinam:
Passo 1
Faaala, galeeera! Tudo tranquilo por aí?
Você se lembra o que significa união e interseção de conjuntos? Basicamente união é você somar os conjuntos e interseção são os elementos que conjuntos compartilham. E quando a gente faz uma subtração de conjuntos do tipo , eu tô dizendo basicamente que eu quero saber quais são os elementos EXCLUSIVOS de J!!
Além disso, precisamos lembrar que por exemplo, aquela barra que tem ali em cima significa que são os elementos que pertencem ao universo tal que esses elementos NÃO pertençam a A.
Passo 2
Vamos começar com os mais tranquilos que são as uniões, interseções e exclusividades dos conjuntos.
Na letra (A) queremos a interseção dos conjuntos, e, portanto, temos que ver qual região interliga todos os conjuntos. Essa região é a de número (1), certo?
Na letra (B) queremos a união dos conjuntos, portanto, bastaríamos somar as regiões (2)+(1)+(3).
Passo 3
Agora vamos olhar o na letra (d). A gente viu que são os elementos que pertencem ao universo tal que esses elementos NÃO pertençam a A, ou seja, é tudo menos o que tá em A.
Por analogia na letra (e) é tudo menos o conjunto B, logo:
Passo 4
(f) Note que agora que a gente entendeu o que significa essa barrinha em cima do conjunto, fica super mais tranquilo de entender. Por exemplo, na letra f, queremos tudo menos a interseção do conjunto A e B. Quem é mesmo a interseção do conjunto A e B?? Vimos lá na letra (a) que seria a região (1), então podemos dizer que o que procuramos é o universo menos essa região.
Passo 5
(g) Analogamente, podemos dizer que agora queremos o universo menos a região da união dos conjuntos, ou seja:
Passo 6
Em (h) e (i), primeiro temos que saber quais são os elementos exclusivos de A e B, respectivamente, ou melhor, quais são as regiões exclusivas de A e B? e , concorda?
Agora quando colocamos a barrinha em cima o que queremos dizer mesmo? Queremos tudo menos essas regiões.
Resposta
- (1)
- (2) +(1) +(3)
- (2)