Nos diagramas seguintes, pintar as regiões que determinam o conjunto , em cada caso.
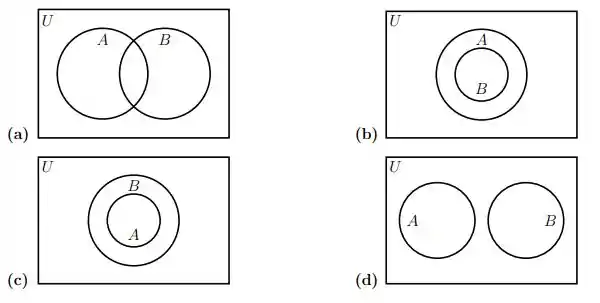
Passo 1
Faaala, galeeera! Tudo tranquilo por aí?
Aqui precisamos lembrar que intersecção representa aquela região onde os conjuntos dividem os elementos.
Passo 2
Na letra (a) esse espaço é:
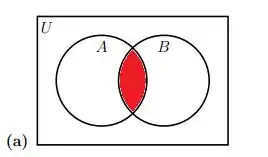
Passo 3
Na letra (b) observa que A está CONTIDO em B, ou seja, no fundo, A é uma intersecção com B, afinal de contas, ele divide elementos com B. Analogamente na letra (c), B está contido em A e divide elementos com A, portanto, é uma intersecção.
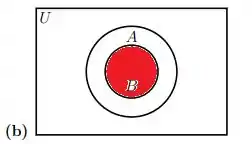

Passo 4
Por sua vez, na letra (d) não há intersecção entre os conjuntos A e B. Observe que eles nem se tocam, o que é um requisito mínimo para que possamos começar a pensar em intersecção de conjuntos, beleza?
Resposta
Demonstração