UFSC, Pré-cálculo – Lista 1 – Questão 20
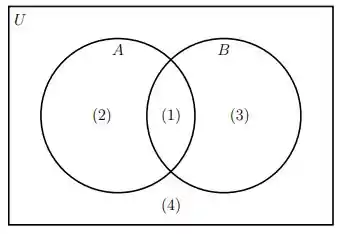
Usando o diagrama de Venn-Euler do exercício anterior. Usando apenas os conjuntos A, B e seus complementares e apenas a operação de interseção, caracterize cada uma das quatro regiões do diagrama. Exemplo: A região (1) é dada por
Passo 1
Vamos primeiro buscar o diagrama da questão anterior hahaha
Agora que ele tá aqui, podemos respirar e finalmente te perguntar se está tudo bem com você! Ahaha
Bem, nessa questão podemos resolver diversas formas, afinal de contas, uma região pode ser definida de formas distintas.
Passo 2
Por exemplo, se eu quisesse somente a região (2). Você concorda comigo que ela seria somente os elementos que pertencem a A, ou seja, seriam os elementos EXCLUSIVOS de A. Isso pode ser calculado como sendo .
A região (1), o enunciado já deu a dica de como podemos fazer, então vamos pra região (3) que representa também os elementos exclusivos de B e podem ser escritos analogamente ao feito anteriormente, certo? Logo, a região (3) pode ser dita como .
Passo 3
Por sua vez, como eu poderia escrever a região 4? Uma vez que ela é todo o meu domínio!! Toda vez que a gente quiser representa o domínio maior, ou seja, aquele que contém todos os outros subconjuntos, a gente pode usar a famosa notação com barrinha em cima, que significa “complementar”. Ou seja, se eu quiser encontrar a região 4, você concorda comigo que ela é tudo MENOS a soma dos conjuntos A e B?
Opa, soma de conjuntos é uma união, né? E complementar é colocar a barrinha em cima!! Então a região (4) pode ser escrita como:
Show de bola até aqui? Te espero na próxima questão!!!
Resposta
Demonstração