Dizer se é verdadeiro ou falso. No caso de ser verdadeiro, justifique e, no caso de ser falso, corrija a sentença.
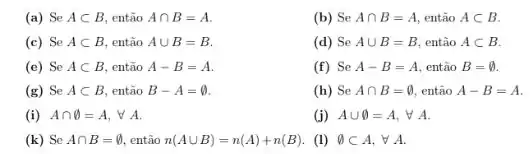
Passo 1
Faaala, galeeera! Tudo tranquilo por aí?
Aqui vamos precisar lembrar bem da teoria de conjuntos!!
Então vamos resolver isso aí!!
Passo 2
- Verdadeiro, pois se um conjunto está dentro de outro (contido) necessariamente ele também é sua intersecção
- Verdadeiro, pois se , e temos que , logo A está contido em B
- Falso, se
- Falso, pois se a união de dois conjuntos dá um dos conjuntos, isso quer dizer que temos um conjunto dentro do outro
- Verdadeiro, pois se indica que queremos apenas os elementos exclusivos de A
- , então é conjunto vazio, logo é verdadeiro
- Verdadeiro, pois se B está contido em A, os elementos exclusivos de B não existem, pois todos pertencem simultaneamente a A e B
- Se não há intersecção entre dois conjuntos, isso quer dizer que os elementos são exclusivos de cada um dos conjuntos, e portanto, , logo é verdadeira a sentença
- Falso, pois se A faz intersecção com conjunto vazio, na verdade não há intersecção
- Verdadeiro, pois se unirmos um conjunto A com um conjunto vazio, seu resultado será apenas um conjunto com elementos exclusivos de A
- Se dois conjuntos não têm intersecção, o número total de elementos da união deles deve ser igual a soma do número de elementos de cada conjunto, logo é verdadeiro.
- O conjunto vazio sempre está contido em qualquer conjunto, logo é verdadeiro.
Resposta
Explicação