Verificar quais dos seguintes conjuntos são conexos
Passo 1
Oiee, tudo tranquilo por aí?
Então, nessa questão recebemos o seguinte conjunto:
Ou seja, é um conjunto cujos pontos são definidos pela inequação:
Precisamos verificar se esse conjunto é conexo.
Um conjunto conexo é aquele que não pode ser separado em dois conjuntos abertos disjuntos, ou seja, que não tem intersecção. Isso significa que o conjunto não pode ser separado em pedações desconectados.
Pra verificarmos isso, tem um bizu muito legal. Vamos desenhar a região no plano e verificar se para quaisquer dois pontos escolhidos conseguimos traçar um caminho entre eles que esteja todo contido dentro da região. Se isso acontecer, o conjunto é conexo, beleza?
Vamo nessa!
Passo 2
Temos que o nosso conjunto é definido por:
Ou seja, o está compreendido em todos os reais e limita-se entre os dois valores acima. Isso representa uma região plana infinita no .
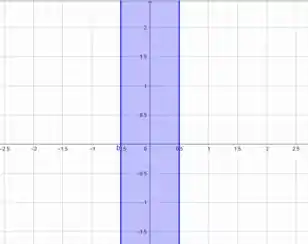
Excelente!
Passo 3
Vamos agora identificar se essa região representa um conjunto conexo ou não.
De cara a gente já pode perceber que ela não possui nenhum pedaço desconectado.
Além disso, se escolhermos dois pontos quaisquer dentro dessa região, sempre é possível traçar um caminho (que não precisa ser uma reta) que pertence à região.
Assim, concluímos que essa região é conexa.
Valeu galerinha 😊
Resposta
Conexa.