UTFPR, Sem Campus, Cálculo Diferencial e Integral 2, Listas de Cálculo 2 - Profº Félix Gómez - Primeira Lista, Questão 1.3d
Identificar as afirmações verdadeiras
O conjunto
é conexo.
Passo 1
Faala gente bonita, tudo beleza?
Nessa questão precisamos verificar se a afirmação:
“O conjunto
é conexo.”
é verdadeira ou falsa, beleza?
Pra começar, vocês lembram o que é um conjunto conexo?
Um conjunto conexo é aquele que não pode ser separado em dois conjuntos abertos disjuntos, ou seja, que não tem intersecção.
Por exemplo, o conjunto:
Conseguimos separá-lo em dois conjuntos abertos?! Poderíamos tentar fazer:
onde .
Aqui nessa questão, conjunto nos foi definido através de uma equação. Vamos primeiramente descobrir os pontos que satisfazem essa equação, para aí sim verificarmos se o conjunto formado por esses pontos é conexo ou não.
Passo 2
Temos:
Completando quadrados no polinômio, temos:
Para o polinômio em , temos:
Juntando tudo, temos:
Essa equação lembra muito uma circunferência, conseguiram perceber? Pois a equação da circunferência é da forma:
Então, aqui é como se tivéssemos o nosso conjunto sendo formado por todos os pontos exteriores à circunferência centrada em e com raio .
Show de bola, já conseguimos localizar espacialmente quem é o nosso conjunto.
Mas, será que ele é conexo?
Passo 3
Então, agora vamos verificar se esses pontos exteriores à circunferência formam um conjunto conexo ou não.
Será que conseguimos separar esse conjunto em dois conjuntos abertos e distintos?
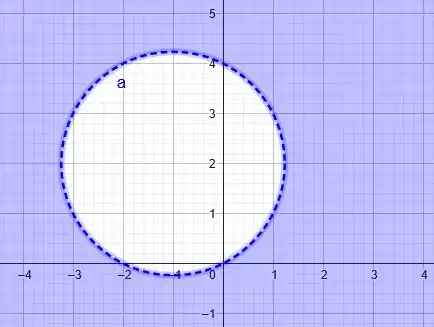
A parte em azul representa o nosso conjunto.
Uma forma muito legal de verificar se um conjunto é conexo, é pensar se para quaisquer dois pontos genéricos existe um caminho que os liga e que está totalmente dentro do conjunto. Esse caminho não precisa ser uma reta.
Isso serve basicamente pra analisar se não existem pedaços desconectados no nosso conjunto, sacaram?
No caso do conjunto acima, sempre existirá um caminho ligando dois pontos genéricos, e que está dentro do próprio conjunto.
Portanto, ele é conexo.
Logo, a afirmação é verdadeira.
Valeeeu pessoal, até a próxima 😊
Resposta
Verdadeira.