Em um universo de 1000 pessoas, foi feita uma pesquisa sobre a respeito do consumo de três produtos A, B e C, obtendo-se os resultados da tabela ao lado. Determine quantas pessoas que consomem:

1. Somente A
2. A ou B
3. A ou B ou C
4. Nenhum dos três produtos

Vamos lá!! O primeiro passo é a gente desenhar os conjuntos e escrever os valores das suas interseções que estão na tabela.

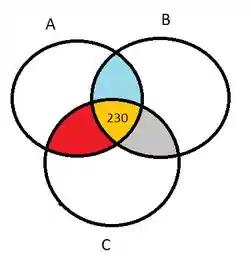
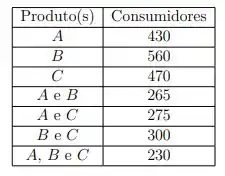
Eu fiz bem colorido pra gente entender tudinho que tá ali! Primeiro passo é a gente começar pela interseção dos três conjuntos que está em amarelo. Agora a gente começa a preencher as outras interseções e olha como a gente vai fazer isso!!

Vamos olhar pra interseção em cinza que são as pessoas que consomem B e C. Na tabela temos 300 pessoas que consomem ambos, porém, note que 230 por ser interseção dos três conjuntos, já está contabilizando pessoas também que tomam A, B e C. Portanto, o que a gente vai fazer agora pra encontrar os valores das outras interseções é: pegar o valor da interseção de dois conjuntos e subtrair das interseções dos 3.

Por exemplo, pessoas que consomem B e C deve ser: 300 – 230 = 70

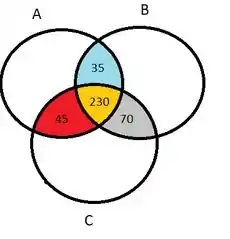
Analogamente, se fizermos isso para as outras interseções teremos:

Agora a gente tem que saber quantas pessoas vão tomar somente A, B ou C. Para fazer isso, a gente vai fazer muito parecido com o que vimos nos passos anteriores, mas agora, a gente vai pegar os valores que estão na tabela pra cada produto individualmente e vai subtrair da soma dos valores das interseções que estão nesse conjunto. Por exemplo, vamos olhar pro A que diz que 430 pessoas consomem ele. As interseções que estão em A estão destacadas abaixo em azul!!

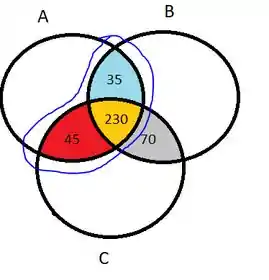
Então para saber quantas pessoas consomem unicamente A, só precisamos fazer:

Analogamente ao passo 4, para pessoas que só consomem B e C, temos que pegar o valor da tabela de pessoas que só consomem esses insumos e depois subtrair da soma das interseções do conjunto.

Uma coisa legal pra verificar se sua conta está certa é agora somar os valores que aparecem no seu diagrama de Venn Euler.

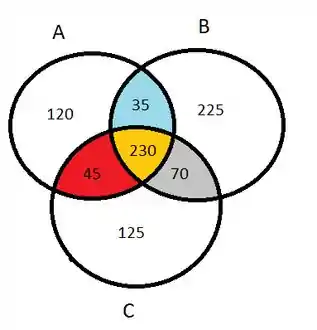
Se a gente fizer ! E eita, isso é menor do que o número de pessoas que foram entrevistadas. Tá faltando aí 150 pessoas pra completar 1000, certo? Essa quantidade que falta é exatamente o número de pessoas que NÃO CONSOMEM NENHUM DOS TRÊS PRODUTOS.

Percebeu que a gente veio desenrolando a questão toda só se questionando sobre como fazer as coisas e concluímos que:

1. 120 pessoas consomem A
2. O número de pessoas que consomem A OU B deve ser igual a todas as pessoas que em algum momento consomem A ou consomem B
3. O número de pessoas que consomem A ou B ou C deve ser igual a
4. 150 pessoas não consomem nenhum dos produtos