UFSC, Pré-cálculo – Lista 1 – Questão 18
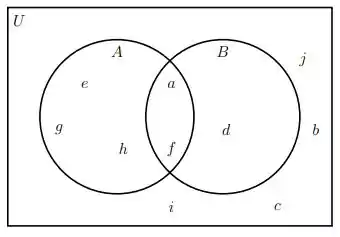
Observando o diagrama de Venn-Euler ao lado, determine:
- B
Passo 1
Faaala, galeeera! Tudo tranquilo por aí?
Você se lembra o que significa união e interseção de conjuntos? Basicamente união é você somar os conjuntos e interseção são os elementos que conjuntos compartilham. E quando a gente faz uma subtração de conjuntos do tipo , eu tô dizendo basicamente que eu quero saber quais são os elementos EXCLUSIVOS de J!! Com isso, a gente agora pode seguir!!
Passo 2
(a) Na letra A queremos saber quem são os elementos do conjunto A, ou seja, tudo o que está na bolota ali do lado esquerdo.
(b) Na letra B queremos saber quem são os elementos do conjunto B, ou seja, tudo o que está na bolota ali do lado direito.
Passo 3
(c) Aqui, queremos a INTERSEÇÃO dos conjuntos. Olhando pro nosso diagrama de Venn Euler, a interseção sempre se dá naqueles elementos que pertencem a A e B ao mesmo tempo, no nosso caso esse conjunto é:
(d) Por sua vez, a UNIÃO é a gente juntar geral!!!!
Passo 4
Na letra (e) e (f), como vimos no passo 1, estamos interessados nos elementos que são exclusivos de A e B, respectivamente.