Considere o plano e as retas
e
Um tetraedro tem um vértice no ponto de intersecção das retas e , tem volume 52 e uma de suas faces, contida no plano , é um triângulo retângulo com ângulo reto em um ponto da reta . Faça uma figura que represente esse tetraedro e determine as coordenadas de seus 4 vértices.
Passo 1
Primeiro vamos fazer a figura que representa esse tetraedro. Temos que:
- Um vértice deve ser o ponto de intersecção das retas e
- Uma de suas faces está no plano e forma um triângulo retângulo (sendo o ângulo reto no ponto da reta )
Então nosso tetraedro pode ser desenhado assim
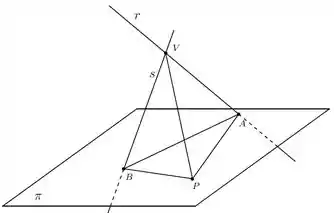
Passo 2
Agora precisamos achar as coordenadas dos 4 vértices.
Vamos começar pelo vértice , fazendo a intersecção das retas e beleza?
Antes de tudo vamos diferenciar os parâmetros, porque não podemos fazer a intersecção se o parâmetro das duas retas for o hehe então
e
Um ponto genérico da reta é e um ponto genérico da reta é .
Para encontrar a intersecção, vamos igualar esses dois pontos:
Isso vai dar pra gente o sistema:
Da última linha, temos que , substituindo na segunda linha temos
Então
Logo, o nosso ponto de intersecção vai ser
Passo 3
Agora vamos encontrar o vértice ok? Ele vai ser a intersecção da reta com o plano .
Vamos pegar aquele ponto genérico da reta que a gente achou no passo anterior e substituir na equação do plano :D
Então o vértice vai ser
Passo 4
E o ponto ?
Ele é a intersecção da reta com o plano né? Então bora fazer a mesma coisa do passo anterior: substituir o ponto genérico de na equação do plano :
Então o ponto vai ser
Passo 5
Agora só falta o ponto hihi
Vamos chamar de .
Antes de tudo:
As informações que temos de são:
- Ele pertence ao plano
- O volume do tetraedro total é 52
Da primeira condição, aplicando o ponto no plano , temos que
Da segunda condição:
E da terceira condição:
Resolvendo o determinante e passando o 6 pro outro lado:
Passo 6
Agora temos que resolver o sistema:
Resolvendo esse sistema, encontramos dois possíveis valores para :
Aeee, encontramos todos os nossos vértices :D