Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Posição Relativa de Reta e Plano

Ver Teoria
Exercício 2012345678910111213141516171819212223242526

Enunciado

USP, P2, 2017, 5

Considere um tetraedro T de vértices A , B , C , D   ∈ E 3 e suponha que as seguintes condições sejam satisfeitas:

I )   A B → = 2   ,   A C → = 3   e   A D → = 5 ;  

I I )   o   t r i â n g u l o   A B C   e s t á   c o n t i d o   n u m   p l a n o   p a r a l e l o   a o   p l a n o   d e   e q u a ç ã o   x - 2 y + 3 z - 1 = 0

I I I )   a   m e d i d a   d o   â n g u l o   B A ^ C   é π 3

I V )   a   m e d i d a   d o   â n g u l o   e n t r e   o   v e t o r   A D →   e   o   v e t o r   n → = 1 , - 2,3   é     π 6  

Temos que o volume de T é igual a:

a ) 15 4      

b ) 5 3 4

c ) 45 2 v

d ) 15 3 2 v

e ) 45 3 2 v

Passo 1

Falaa, blz?? Bora fazer um desenho para nos ajudar a enxergar o problema:

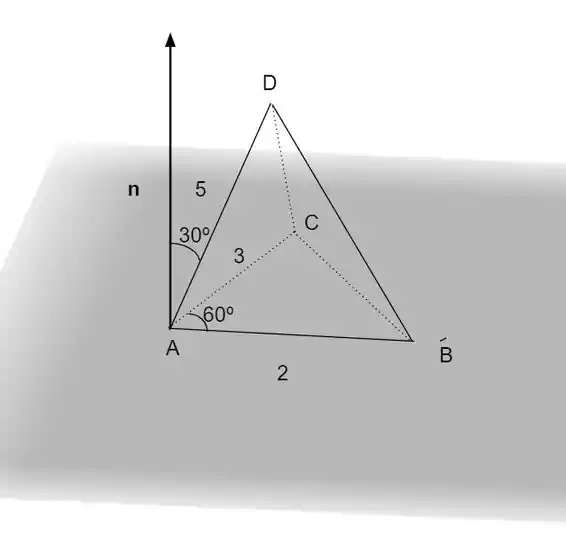
Agora, vamos lembrar que dado um plano a x + b y + c z = d , temos que o vetor ( a , b , c ) é normal ao plano, ou seja:

Onde n → ⊥ x - 2 y + 3 z - 1 = 0 →   n → = ( 1 , - 2,3 )

Passo 2

Bora agora lembrar como se calcula o volume de um tetraedro, para gente saber o que precisamos fazer no problema.

V T =   A B →   ×   A C → ∙ A D →   6

Vamos usar que   A B →   ×   A C → =   A B →   A C →   s e n   ( A B → , A C → )

Ou seja, temos que A B →   ×   A C → ∙ A D → = A B →   ×   A C →   A D → cos ⁡ ( A B →   ×   A C → ,   A D → ) )  

Passo 3

Bora agora ajustar todas as contas.

A B →   ×   A C → =   A B →   A C →   s e n   A B → , A C → = 2 3   s e n π 3 = 6 3 2 = 3 3

Agora basta acharmos A D → cos ⁡ ( A B →   ×   A C → ,   A D → ) )  

O ângulo entre A B →   ×   A C →   e   A D → é qual??

Vamos lembrar que A B →   ×   A C → é um vetor perpendicular a A B →   e   A C → , ou seja, pela figura conseguimos ver que esse vetor é paralelo a n →   , ou seja, o ângulo entre um vetor paralelo a n → e A D → é π 6 , logo:

A D → cos ⁡ ( A B →   ×   A C → ,   A D → ) ) = 5 cos ⁡ π 6 = 5 3 2  

Juntando tudo:

A B →   ×   A C → ∙ A D → =   A B →   ×   A C →   A D → cos ⁡ ( A B →   ×   A C → ,   A D → ) )  

= 3 3     5 3 2 = 45 2

Ou seja:

V T =   A B →   ×   A C → ∙ A D →   6 = 45 12 = 15 4

E assim finalizamos mais um probleminha, bora para o próximo?

Resposta

Letra A

Exercícios de Livros Relacionados

Verifique se a reta ⎧x= 1 - 3 α⎧ r⎢y= 2+ α ⎢ ⎩z= 1-2 α⎩ está contida no plano determinado pelos pontos ( 1,0 , - 1 ) , ( 2,1 , 1 ) e ( 0,3 , 1 ) .
Determine se os planos são paralelos, perpendiculares ou nenhum dos dois. No caso de nenhum dos dois, calcule o ângulo entre eles. 2 x - 3 y + 4 z = 5 , x + 6 y + 4 z = 3
Encontre uma equação de plano para um plano que passe pelo ponto ( 2,0 , 1 ) e seja perpendicular ao vetor x = 3 t , y = 2 - t , z = 3 + 4 t .
Determine as equações paramétricas da reta intersecção dos planos. 5 x - 2 y - 2 z = 1
Determine o ponto no qual a reta intercepta o plano dado. x = y - 1 = 2 z ; 4 x - y + 3 z = 8 .