Verificar se e são perpendiculares, sendo
Passo 1
Temos as equações vetoriais da reta e do plano .
Dados:
Com esses dados devemos verificar se a reta e o plano são perpendiculares.
Mas, como faz isso ??? Na teoria só fala de perpendicularidade quando comparamos o vetor diretor da reta e o vetor normal do plano!!! Não tenho o vetor normal do plano!!

Calma!!! Para tudo tem um jeito, e vamos te ensinar como fazer!!!
Passo 2
Não temos o vetor normal ao plano, massss, nós temos dois vetores que são paralelos ao plano. Assim, se fizermos o produto vetorial desses dois vetores, encontraremos o vetor normal ao plano. Blz? Bora, fazer o produto vetorial então!!
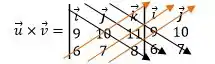
Passo 3
Agora sim, que temos o vetor normal do plano podemos usar nossa teoria para verificar se a reta e o plano são perpendiculares. Para isso devemos ver se:
Vamos checar?
Como
Portanto, a reta e o plano não são perpendiculares.