Dados os planos e , a reta e o ponto :
a) Encontre a equação geral de .
b) Qual a posição relativa entre e ? Justifique sua resposta.
Passo 1
a) Para encontrarmos a equação geral de , precisamos calcular o seguinte determinante:
Onde é um ponto do plano, enquanto e são vetores diretores.
Eita mas a gente já tem a equação vetorial do plano , então podemos tirar essas informações de lá:
Passo 2
Substituindo os dados no determinante:
Então, a equação geral de é
Passo 3
b) Pelas equações de e de , sabemos que um vetor diretor de é e um vetor normal de é .
Fazendo o produto escalar entre esses dois vetores:
Logo, e são perpendiculares.
Isso quer dizer que , e consequentemente , é paralelo ao plano , mas precisamos testar algum ponto de no plano pra ver se ela está contida nele demorou?
Substituindo o ponto na equação geral do plano :
Logo, como o ponto de não pertence a , não está contida no plano. Então ela é apenas paralela a ele, como mostra o esboço abaixo :P
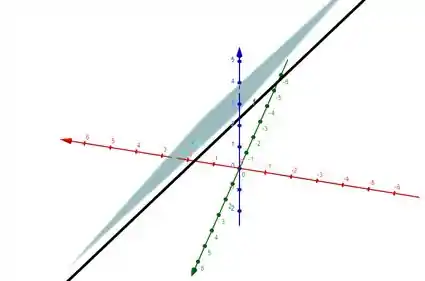
Resposta
a)
b) Paralelos.