Ache equações paramétricas da reta que passa por e é perpendicular à reta

Com os dados que temos podemos desenhar nosso problema da seguinte maneira:

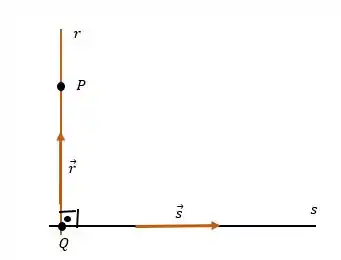
O vetor diretor da reta conseguimos retirar pelas equações simétricas . O ponto é dado, . E a última informação preciosa que temos é que as retas são perpendiculares, ou seja, formam e são concorrentes.

Mas, como acho o vetor diretor da reta ??

Como sabemos que as retas são perpendiculares, então, seus vetores diretores também são. Se são perpendiculares, o produto interno entre eles deve ser ZERO.

O ponto de interseção entre as reta é . Como pertence à reta , então um ponto genérico de é:

Então:

O vetor diretor de será então o vetor formado pleos pontos e :

Assim, se e , temos que fazer o produto interno entre eles e deve dar ZERO.

Resolvendo o produto interno:

Pronto achamos o vetor diretor da reta :

Agora que já temos o vetor diretor e um ponto que pertence à reta , falta escrevermos as equações paramétricas de .

Multiplicando por