Verifique se as retas
são ortogonais. Verifique também se são perpendiculares.
Passo 1
Temos novamente a equação vetorial de duas retas. Mas, agora queremos saber se as retas são ortogonais e se forem, se são perpendiculares também. Vamos retirar então o que temos de informação sobre cada reta:
Dados:
Passo 2
Como vimos na teoria, para verificar se duas retas são ortogonais temos que verificar se o produto interno entre elas é ZERO.
Como o produto interno deu ZERO, então as retas são ortogonais. Será que são perpendiculares também?! Vamos verificar!!
Passo 3
Para saber se duas retas são perpendiculares, precisamos verificar se elas são concorrentes, ou seja, possuem um ponto em comum. Assim, temos duas possibilidades: Ver se as retas são concorrentes ou verificar se possuem um ponto em comum. Vamos fazer pelos dois jeitos.
Vamos começar verificando se são concorrentes!!
Analisando os vetores diretores das retas, vemos que e não são proporcionais. Assim, as retas não são paralelas. Mas, elas podem ser concorrentes ou reversas. Assim, vamos montar o produto misto para verificar isso:
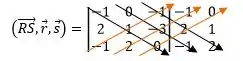
Como o produto misto deu DIFERENTE DE ZERO, então as retas são reversas. Logo, não são perpendiculares.
Passo 4
Outra maneira de verificar a perpendicularidade é ver se as retas possuem algum ponto em comum. Para isso, vamos igualar as coordenadas das retas para ver se encontramos algum ponto possível:
Igualando teremos:
Pelo , chega-se que . Substituindo esse valor na equação de , temos:
Já temos os valores de e . Só falta testar se esses valores também satisfazer a equação do :
Os valores não satisfazem. Assim, as retas não possuem nenhum ponto em comum. Logo, não são perpendiculares.