Considere as retas e
a) Escreva equações paramétricas para a reta .
b) Mostre que e são concorrentes.
c) Escreva equações paramétricas para a reta que corta e perpendicularmente.
Passo 1
a) Primeiramente, a gente pode somar as duas equações que definem a reta , obtendo
Beleza, a gente encontrou em função de , então bora substituir isso na primeira equação de ? (pode ser na segunda também, você que sabe :P)
A primeira equação é
Substituindo pela expressão
Vamos isolar a variável
Passo 2
Ok, precisamos de um ponto pertencente à reta para encontrarmos sua equação paramétrica. Pra isso, vamos atribuir um valor qualquer a para aí encontrarmos os valores de e .
Se atribuirmos (novamente, você que escolhe o valor :P):
Da expressão teremos que
E da expressão teremos que
Passo 3
O ponto nós já temos, agora só falta o vetor diretor.
Atribuindo (sendo que esse 1 vem do ponto que encontramos no passo anterior) e substituindo, respectivamente, em e :
Logo, a equação paramétrica de vai ser
Sendo que o vetor diretor de é
Passo 4
b) Pra que as duas retas sejam concorrentes, elas devem ter um ponto de intersecção, ou seja, tem que existir algum ponto onde , e são iguais, assim:
Da expressão , a gente chega que
Substituindo na expressão , temos que , então o também vale 1 certo?
Substituindo e na expressão , chegamos que , o que é verdadeiro, logo, esse sistema possui solução e então e de fato possuem um ponto de intersecção :D
Pra encontrar esse ponto de encontro é só substituir ou na equação de qualquer uma das retas, o ponto encontrado vai ser .
Passo 5
c) Ta, antes de qualquer coisa, vamos ver a figura abaixo
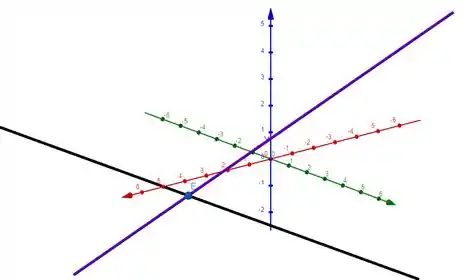
Aqui é a reta preta, é a reta roxa e o ponto é o ponto que encontramos no item anterior.
Pra uma reta cortar e ao mesmo tempo de maneira perpendicular, ela precisa necessariamente passar pelo ponto .
Além disso, o vetor diretor de vai ser o produto vetorial do vetor diretor de com o vetor diretor de , isso porque esse produto vetorial com certeza vai ser perpendicular às retas, e isso é o que queremos ;)
Passo 6
Sabemos que o vetor diretor de é enquanto o de é .
Bora fazer o produto vetorial deles pra encontrar o vetor diretor de :
Então, o vetor diretor de vai ser
Passo 7
Sabendo que passa pelo ponto e sabendo seu vetor diretor, podemos escrever sua reta paramétrica:
O desenho fica assim (sendo a reta verde)
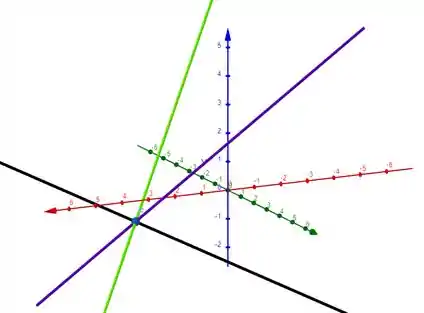
Resposta
a)
b) Demonstração.
c)