Sejam as retas e .
a) Determine a posição relativa entra as retas e .
b) Determine as equações paramétricas para a reta perpendicular comum às retas e .
Passo 1
a) Antes vamos observar os vetores diretores das retas: e .
e não são múltiplos, pois não existe tal que . Logo, já sabemos que as retas não são paralelas.
O próximo passo é fazer o produto misto entre , e , sendo um ponto de e um ponto de .
Passo 2
De acordo com a equação das retas, o ponto pertence à reta , assim como o ponto pertence à reta .
Logo, o vetor é
Passo 3
Calculando o produto misto :
Opa, o produto misto deu 0!! Então as retas poderiam ser concorrentes, paralelas distintas ou iguais certo?
Porém já vimos lá no passo 1 que e não são paralelos, logo as retas não podem ser nem paralelas distintas e nem iguais.
Ou seeeja, elas são CONCORRENTES!! :D
Abaixo temos em laranja a reta e em verde a reta
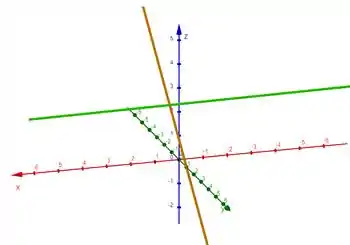
Passo 4
b) Essa reta perpendicular a e vai ter como vetor diretor o produto vetorial de e (pois este vai ser perpendicular às duas retas) e vai passar pelo ponto de intersecção entre as duas retas beleza?
Primeiro vamos encontrar a intersecção de e , para isso, vamos trocar o parâmetro de pelo parâmetro beleza? Então nossas retas são:
Um ponto genérico de é e um ponto genérico de é . O ponto de intersecção das retas vai ser dado quando :
Igualando cada coordenada, temos o sistema:
Passo 5
Da terceira equação, temos que . Vamos substituir isso na segunda equação:
(a gente também poderia ter encontrado o , no final o ponto de intersecção vai ser o mesmo)
Boaaa, então o ponto de intersecção de e vai ser dado quando no ponto genérico :
Então já sabemos que a reta , perpendicular a e , vai passar pelo ponto :D Agora vamos encontrar o vetor diretor dela.
Passo 6
Fazendo o produto vetorial :
Ou sejaa, a reta vai ter como vetor diretor o vetor
Passo 7
Já temos tudo que precisamos para escrevermos a equação paramétrica da reta :
Abaixo temos em preto a reta :
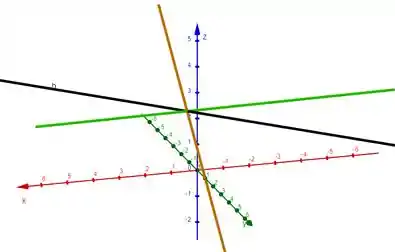
Resposta
a) Concorrentes
b)