Sejam e as retas reversas, passando por e e por e respectivamente. Obtenha uma equação vetorial da reta , concorrente com e , e paralela ao vetor .
Dados: e .
Passo 1
Preparado para mais um exercício sobre posição de retas??

Isso aí!! Nesse exercício vamos utilizar algumas estratégias que ainda não usamos. Então, bora começar!!
Vamos retirar os dados do enunciado:
Dados:
Além disso, e são reversas, ou seja, retas que não são paralelas e não tem ponto em comum.
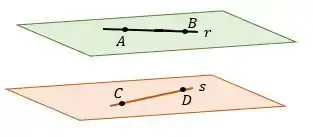
O enunciado disse que é concorrente com e , e paralela ao vetor .
Se é concorrente com e , é porque existe uma ponto comum entre (que chamaremos de ) e um ponto em comum entre (que chamaremos de ). Com esses dados podemos desenhar o seguinte esquema:
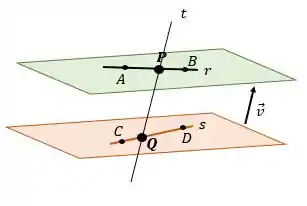
Passo 2
Criamos os pontos e que pertencem a reta , mas não temos nenhuma informação sobre eles. Como também pertence a e também pertence a , para sabermos a cara desses pontos precisamos das equações gerais das retas e .
Vamos começar com a reta :
A e essa reta é formada pelos pontos e podemos escrever que seu vetor diretor é e que o ponto pertencente à reta é . Poderia ter escolhido o vetor como diretor, como o ponto como pertencente à reta. Calculando , podemos escrever a equação geral da reta :
Com a expressão vetorial da reta , podemos escrever o ponto que será da forma:
Beleza?!
Faremos o mesmo para determinar o ponto , mas agora com a reta :
Os pontos e pertence a reta e podemos escolher o vetor diretor e o ponto , para encontrar a equação geral de :
Escolhendo o ponto , Temos que a reta como:
Com a expressão vetorial da reta , podemos escrever o ponto que será da forma:
Pronto!! Temos e . Lembrando que escolhemos e porque são diferentes retas, logo, não podemos usar o mesmo parâmetro.
Passo 3
Agora que temos e , vamos para a segunda parte da resolução!!
Pelo enunciado sabemos que a reta é paralela ao vetor . Se é paralela à , também paralelo ao vetor formado pelos pontos e , Logo temos que é paralelo ao vetor :
Vamos encontrar primeiro o vetor (que será em função de e ):
Substituindo os valores em :
Podemos montar sistema com três equações e três incógnitas e
Isolando na segunda equação temos
Substituindo o valor de na equação e encontrando o valor de :
Tendo , encontramos o valor de :
Substituindo e na equação , temos o valor de :
Chegamos nos três valores:
Agora podemos substituir esses valores para encontrar os pontos e :
Passo 4
Está quase terminando!! Só falta escrevermos a equação vetorial!! Temos o vetor diretor que é e temos dois ponto: e . Escolhendo qualquer um deles, por exemplo, , escrevemos a equação vetorial: