UFPE – Geometria Analítica – 2018.2 – P1 – Questão 3
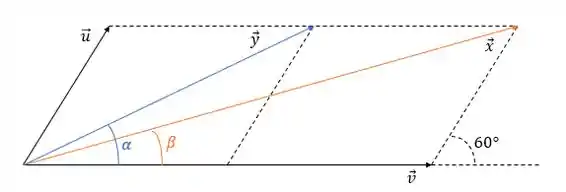
Considere vetores e tais que e e . Se , , e , determine e e represente todos esses vetores e ângulos em uma figura.
Passo 1
Gente, ângulo lembra o que em geometria analítica? Só pode ser produto escalar!
Precisamos achar o produto escalar do numerador.
E também o valor do módulo de !
Daí,
Passo 2
Para o ângulo vamos fazer igualzinho!
Primeiro achamos o produto escalar do numerador.
E depois o valor do módulo de !
E então,
Passo 3
Agora só falta a gente representar esses vetores!
Resposta
Exercícios de Livros Relacionados
Em relação ao produto interno do Exemplo de 8.3.2 calcule x de modo que o ângulo entre 1 - 1 2 1 e 1 - 1 2 x tenha uma medida de 90 ° .
Seja β = { 1,2 , ( 2,1 ) } . Use o processo de Gram-Schmidt para achar uma base ortonormal β ' de R 2 em relação ao produto interno usual.
Seja V = R 2 . Sejam v 1 = ( x 1 , y 1 ) e v 2 = x 2 , y 2 . Se f v 1 ,v 2 = 2 x 1 x 2 + x 1 y 2 + x 2 y 1 + y 1 y 2 , mostre que f é um produto interno.
Considere em R 3 o produto internox , y , z , x ' , y ' , z ' = x x ' + 5 y y ' + 2 z z ' Verifique se realmente é um produto interno.A partir da base { 1,0 , 0 , 0,1 , 0 , ( 0,0 , 1 ) } ache uma base
Seja V = R 3 e S = { 1,0 , 1 , 1,1 , 0 , ( 2,1 , 1 ) } .Encontre S ⊥ .Encontre uma base ortogonal para S e S ⊥ .Se S fosse [ 1,0 , 1 , 1,1 , 0 , 2,1 , 1 ] , qual seria S ⊥ ? Neste caso, encontre uma b