2) Considere a função cujo gráfico é metade de uma semicircunferência, como esboçado abaixo:
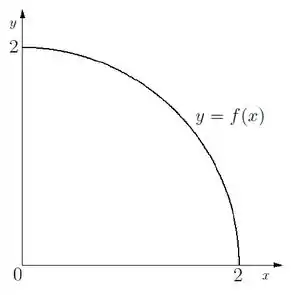
- Determine a expressão da função
- Determine a equação da reta tangente ao gráfico de que é paralela .
Passo 1
Pra começar, vamos achar quem é essa tal de . Veja bem, como temos uma semicircunferência e a equação do círculo é:
Onde é o centro da circunferência e é o raio, como ela está centrada na origem e temos raio igual à vamos ter:
Escrevendo como uma função de , ficamos com:
Opa, peraí. Duas equações? Pois é, temos uma versão positiva e outra negativa. Como a semicircunferência que queremos está acima do eixo , a expressão de então vai ser a versão positiva, beleza? E logo:
Passo 2
Agora bora achar a equação da reta tangente. De forma geral, uma reta tangente tem a seguinte fórmula:
Onde é o ponto de tangência e é a inclinação da reta tangente. Ok, mas e daí? Veja bem, se a reta tangente que queremos é paralela à:
Então a inclinação vai ter que ser a mesma! O valor de então já sabemos, vai ser:
Mas e o ponto de tangência? Como achar? Veja bem, a primeira derivada de uma função nos dá exatamente a inclinação da reta tangente, não é mesmo? Então, no ponto de tangência:
Derivando nossa então, pela regra da cadeia, temos:
E logo, o valor de vai ser:
Só que aí vamos descartar porque ta dentro do primeiro quadrante, beleza? Sendo assim:
E pra fechar com chave de ouro, vai faltar só a gente achar . Como , vamos ter:
Show de bola, a equação da reta tangente vai ser então: