Considere a função definida pelo gráfico abaixo, a reta tangente ao gráfico da em e a reta tangente ao gráfico em .
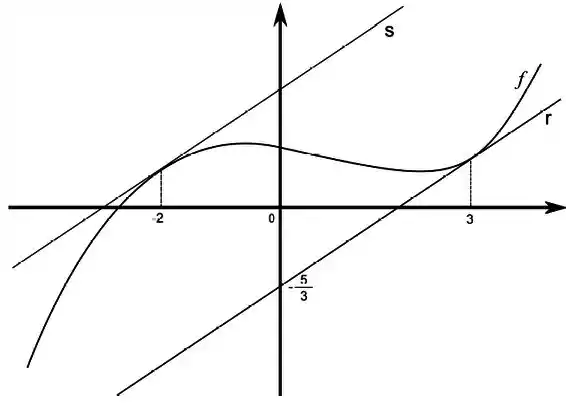
Sabendo , e a reta é paralela à reta , determine:
- A equação da reta
Passo 1
A reta é tangente à função no ponto . Se é tangente seguirá a equação geral da reta tangente:
Como o ponto de tangência é :
O valor de foi dado no enunciado, então podemos substituir também:
Passo 2
Falta só o valor do coeficiente angular, .
Agora vai entrar a ideia das retas paralelas. O enunciado disse que as retas e são paralelas, ou seja, possuem o mesmo coeficiente angular.
O coeficiente angular da reta é que foi dado no enunciado. Dessa forma:
Pronto, já temos tudo que precisamos!
Para ficar bonitinho:
Passo 3
Já vimos ali no passo que a derivada vai ser
Passo 4
Para achar o valor de vamos olhar a reta tangente que passa por , a reta .
Conhecemos um ponto que passa por essa reta, é aquele na parte de baixo, onde a reta corta o eixo , . A equação da reta tangente vai ser:
Passo 5
Vamos agora trocar o valor de e por aquele ponto que pertente a reta: