Admita que, em determinada localidade, se um trabalhador do comércio ficar desempregado, a probabilidade de que ele consiga um novo emprego similar dentro de 6 meses é de 0,6. Caso contrário (com probabilidade 0,4), ele abre seu próprio negócio. Sabe-se também que, tendo conseguido um novo emprego assalariado, em 5% das vezes sua família troca as crianças de colégio. Já os que montam seu próprio negócio trocam suas crianças de colégio em 15% das vezes. Se neste local for selecionado um trabalhador do comércio recém-desempregado:
a)Qual a probabilidade de que suas crianças mudem de escola?
b)Dado que as crianças de fato trocaram de escola, qual a probabilidade de que ele tenha conseguido um novo emprego?
Passo 1
Hum... Achou confuso? Vamos fazer um diagrama pra ajudar a compreensão?
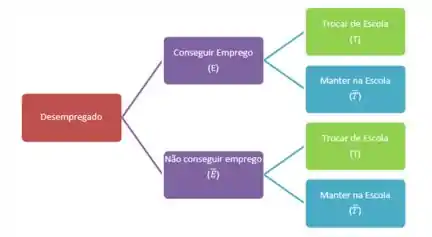
Passo 2
Vamos completar esse diagrama com as probabilidades dadas no enunciada (Tanto as ditas quanto as implícitas!). Ué, como assim?
Bom, se ele fala que a probabilidade de trocar de escola quando se consegue um emprego é de 5%, ele também está falando que a probabilidade não trocar de escola quando se consegue um emprego é .
Entendeu? Temos que olhar sempre o complementar...
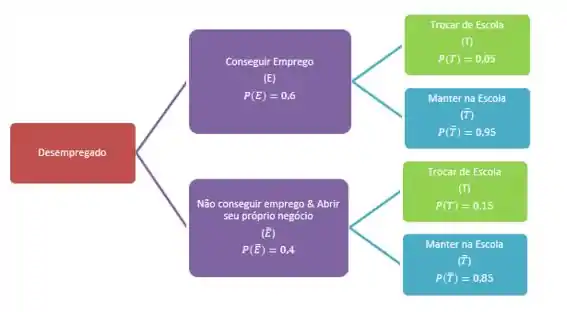
Passo 3
Agora com nosso diagrama já completinho vamos ver o que ele pede...
a)
Queremos saber a probabidade de que suas crianças mudem de escola. Ou seja,
Sabemos que
Passo 4
Utilizando o Teorema da Probabilidade Total temos que:
Substituindo:
Passo 5
b)Dado que as crianças de fato trocaram de escola, qual a probabilidade de que ele tenha conseguido um novo emprego?
Epa! Atenção!!! Ele está falando/afirmando que as crianças trocaram de escola. Sabendo disso queremos a probabilidade dele ter conseguindo um novo emprego, ou seja:
Pela fórmula da probabilidade condicional, teremos:
Passo 6
Pelo Teorema de Bayer:
Assim
Substituindo:
Resposta
a) 0,09
b)