Em uma determinada fábrica constatou-se em registros passados, que uma determinada máquina para a produção de parafusos funciona corretamente do tempo. Se a máquina não está funcionando corretamente, dos parafusos produzidos são defeituosos, e quando a máquina estiver trabalhando corretamente, apenas dos parafusos são defeituosos. Pede-se:

1. Se um parafuso é escolhido aleatoriamente, qual é a probabilidade de que ele não esteja defeituoso?
2. Uma vez que o parafuso não esteja defeituoso, qual é a probabilidade de que este pertence a máquina que esteja funcionando corretamente.

Observação: utilize o teorema de Bayes.

Vamos iniciar nosso problema fazendo um diagrama de árvore, que nos permite visualizar o problema de uma maneira mais direta e simples.

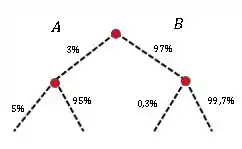
Assim vamos trabalhar da seguinte maneira. Temos duas classes de parafusos, Defeituosos (D) e Não Deteituosos (ND).

Assim se quiséssemos calcular a probabilidade de que uma parafuso não seja defeituoso, teríamos

Ou seja

Que é a probabilidade de o Lado A produzir uma peça defeituosa mais a probabilidade do lado produzir uma peça defeituosa.

Assim temos que

Que é a probabilidade de a maquina estar com defeito vezes a probabilidade dela não produzir uma peça seja defeituosa + a probabilidade dela não estar com defeito vezes a probabilidade dela não prodizir peça defeituosa (Basta ver que seguimos o caminho do diagrama).

Assim podemos finalmente calcular dizendo que

Agora vamos utilizar o teorema de Bayes para determinar qual é a probabilidade de que a maquina que esteja funcionando perfeitamente (B) pertença a classe (ND). Ou seja,

A probabilidade de a maquina com que funciona perfeitamente produzir peças ssem defeito dividido pela probabilidade de existir peças sem defeito no geral.

Interessante que acabamos de calcular , assim só precisamos calcular a probabilidade de a maquina sem defeito produzir peças sem defeito.

Ou seja

Assim temos que pelo Teorema de Bayes