Uma empresa de desenvolvimento urbano considera a possibilidade de construir um shopping center num setor no Rio de Janeiro. Um elemento vital é uma proposta em um setor com estrada que liga ao centro da cidade.
Se o Conselho aprovar essa rodovia, há probabilidade de de a empresa construir o shopping, enquanto, se a rodovia não for aprovada a probabilidade é de apenas . Com base em informações disponíveis, o presidente da empresa estima uma chance de de que a estrada seja aprovada.
Pergunta-se:
a) Qual é a probabilidade de a empresa construir o shopping? Mostre o evento correspondente através do Diagrama de Venn (partição do espaço amostral).
b) Uma vez que o shopping foi construído, qual é a probabilidade de que a rodovia não seja aprovada?
Passo 1
Pronto para uma questão sobre probabilidade condicional e teorema de Bayes? Bora que o RespondeAí vai te ajudar!
Antes de discutir o enunciado com você, deixa eu te lembrar a definição de probabilidade condicional. Vamos considerar dois eventos e . A probabilidade de acontecer dado que aconteceu é
Ou seja, a probabilidade condicional de acontecer dado que aconteceu é a probabilidade de ambos os eventos acontecerem sobre a probabilidade do evento acontecer.
Feita essa consideração, vamos o problema: se a rodovia for construída, a probabilidade de o shopping ser construído é . Por outro lado, se a rodovia não for construída, a probabilidade de o shopping ser aprovado cai para . Já a probabilidade de a rodovia ser construída é .
O problema quer saber qual a probabilidade de o shopping ser construído. Como resolver esse problema? Vou escrever um negócio, pensa aí e vê se você concorda:
A probabilidade de o shopping ser construído é a probabilidade de o shopping ser construído junto com a estrada somada a probabilidade de o shopping ser construído sem a estrada.
Passo 2
O enunciado forneceu para gente as probabilidades condicionais:
Usando a definição de probabilidade condicional que eu mostrei no passo 1:
Mas o problema também forneceu que a probabilidade de a estrada ser construída é , de modo que
Com isso, temos
Somando as duas:
Desta forma, a probabilidade de o shopping ser construído é
Passo 3
Apresento para você o Diagrama de Venn da situação:
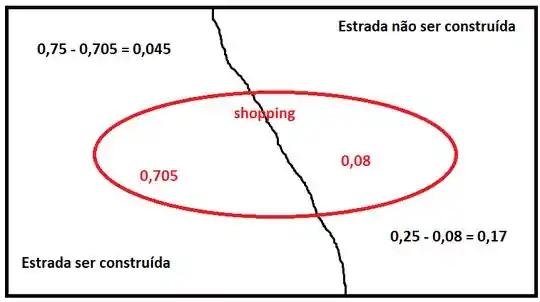
Dentro da região vermelha temos a situação em que o shopping é construído: probabilidade de haver shopping e estrada e probabilidade de haver o shopping sem haver a estrada.
Como a probabilidade de haver a estrada é , a probabilidade de haver a estrada sem o shopping é . Além disso, como a probabilidade de não haver estrada é , a chance de não haver nem shopping nem estrada é . Esses casos são representados fora da região vermelha.
Passo 4
Partiu item (b)!!!
A pergunta é: Uma vez que o shopping foi construído, qual é a probabilidade de que a rodovia não seja aprovada?
Isso é uma probabilidade condicional:
Aqui vamos precisar do teorema de Bayes:
A ideia é a seguinte, sabemos a probabilidade condicional e queremos . Para inverter as relações, usamos o teorema de Bayes:
Sabemos que e , de modo que
Portanto,
Essa é a resposta do item (b) 😉.