Uma urna contém 3 moedas onde uma tem duas caras, outra é uma moeda justa, e a terceira é uma moeda viciada com probabilidade de cara igual a 0,75. Uma moeda é selecionada aleatoriamente da urna e lançada uma vez, tendo se observado o resultado cara. Qual a probabilidade da moeda escolhida ter duas caras?
Passo 1
Hmmm... Temos um evento que já aconteceu (o lançamento de uma moeda e seu resultado cara), e queremos “voltar no tempo” e descobrir se essa moeda lançada foi a moeda que tinha duas caras. Isso tá com cara de que mesmo? Teorema de Bayes!
Lembrando a fórmula dele:
Mas antes de aplicar valor nessa fórmula, bora organizar a notação dos eventos que vamos usar nessa resolução:
Então o que a questão tá pedindo pra gente é:
A probabilidade de a moeda lançada ter sido a com duas caras, sabendo que o resultado do lançamento foi cara! Aplicando isso aí na fórmula do Teorema de Bayes:
Vamos precisar descobrir quem são essas probabilidades aí na fração pra descobrir nossa condicional de interesse então. Vem comigo!
Passo 2
Passo 3
Começando por:
Que nada mais é que a probabilidade de termos cara como resultado, dado que a moeda lançada é a moeda com duas caras. Opa! Se só tem cara na moeda, a probabilidade de sair uma cara dela é de 100%, certo? Então:
E essa probabilidade aqui?
A probabilidade de a moeda lançada ser a com duas caras. Como temos 3 moedas, a moeda com duas caras é 1 em um total de 3, ou seja:
E a probabilidade de termos cara como resultado?
Reparem que é a probabilidade de qualquer cara acontecer, ou seja, a cara pode ser proveniente de qualquer uma das 3 moedas! Vamos fazer um diagrama pra enxergar melhor como calcular isso:
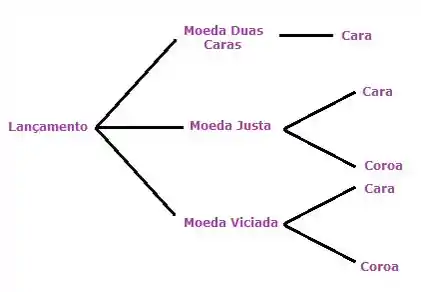
E vamos completar as linhas pretas desse diagrama com a probabilidade do evento que está ao final dessa linha acontecer, assim ó:
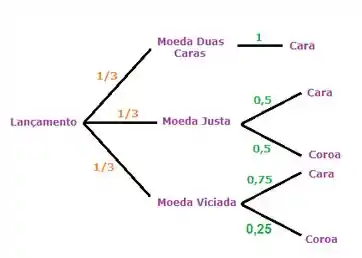
Tranquilin? Lembrando que essas probabilidades em verde são as condicionais!
- Cada moeda tem de chance de ser escolhida
- Moeda com duas caras tem 100% de chance de dar cara
- Moeda justa tem 50% de chance pra cada lado
- Moeda viciada tem 75% de chance de dar cara, e 25% de chance de dar coroa
Agora, para calcular a probabilidade de obtermos uma cara, independente de qual moeda foi escolhida, vamos fazer:
E olhando pro nosso diagrama, podemos substituir essa galera pelos seus respectivos valores:
Passo 4
E finalmente, podemos substituir todas as probabilidades calculadas na fórmula do Teorema de Bayes: