Uma fábrica de televisores compra 2/5 de transistores que necessita de um fornecedor que garante uma confiabilidade (probabilidade de funcionar corretamente sem defeitos) de 80% ao seu material durante um certo período.
A aquisição do restante material é igualmente dividida por duas outras firmas que garantem, respectivamente, confiabilidades de 60% e 70% durante o mesmo período de tempo. Pede-se:
- Seleciona-se ao acaso um transistor do estoque da fábrica para o teste. Qual a probabilidade dele funcionar corretamente? Mostre o evento correspondente através do Diagrama de Venn (partição do espaço amostral).
- Qual a origem mais provável de um transistor que escolhido ao acaso do estoque, se verificou ter funcionado mal?
Observação: utilize o teorema de Bayes.
Passo 1
Primeiro vamos organizar todas as nossas probabilidades. A probabilidade do transistor vir do primeiro fornecedor é:
E a probabilidade de vir dos outros dois tem que ser, juntas, complementar a e valer a mesma coisa, então:
Então a probabilidade de vir do fornecedor 2 e do fornecedor 3 é:
Agora vamos organizar as confiabilidades de cada um dos transistores. Sabemos a confiabilidade de um transistor, dado que veio de certo fornecedor, ou seja... estamos trabalhando com probabilidades condicionais! Vamos representar como o evento “transistor funcionando bem”. Então:
Passo 2
a)
A questão está pedindo a probabilidade do transistor funcionar bem, ou seja:
Nós conhecemos todas as condicionais que estão relacionadas a esse evento, então vamos usar o teorema da probabilidade total:
Substituindo todos os valores:
E como ficaria nosso diagrama de Venn?
Sabemos que todo o espaço amostral tem que ser descrito pelos três fornecedores, já que eles representam todas as possibilidades possíveis. Também sabemos que esses eventos são mutuamente exclusivos, já que um transistor não pode ter vindo de dois fornecedores diferentes. Então:
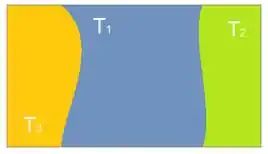
E o evento pode acontecer para qualquer um dos fornecedores, então teríamos algo assim:
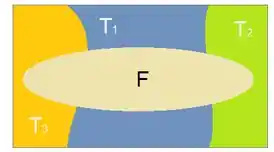
Passo 3
b)
Agora vamos calcular a probabilidade do transistor ter vindo de cada um dos fornecedores, dado que não funcionou bem, e comparar os resultados. Vamos usar como o evento não funcionou bem, já que ele é complementar a :
Usando probabilidade complementar, também podemos calcular:
Agora já temos informações suficientes para calcular a probabilidade de ter vindo de um fornecedor, dado que não funcionou bem.
Começando pelo primeiro fornecedor, e aplicando o teorema de Bayes:
Agora para o segundo:
E o terceiro:
Comparando os valores, vemos que o mais provável é o vir do fornecedor 2, dado que não funcionou bem. O fornecedor 2 é o que tem 60% de confiabilidade.
Resposta
a)
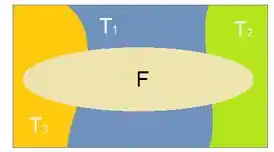
b)
Ter vindo do fornecedor com 60% de confiabilidade.