Aplicando a transformada inversa de Laplace na função , obtemos a função:
( )
( )
( )
( )
( )
Passo 1
Opa, vamos lá. Para calcular essa transformada inversa, podemos dar uma olhada na tabela para acharmos o que mais se aproxima, certo?
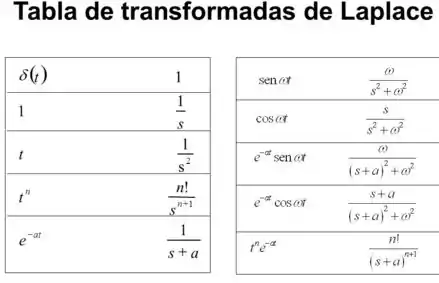
A função com a transformada parece ser bem próximo do que queremos. Só pra lembrar a nossa função é:
Vamos escrever mais parecido com o que temos na tabela:
Logo, a nossa função ficará:
Resposta
Exercícios de Livros Relacionados
Em cada um dos problemas de 1 a 10, encontre a transformada de Laplace inversa da função dada.5. F s = 2 s + 2 s 2 + 2 s + 5
Em cada um dos problemas de 1 a 10, encontre a transformada de Laplace inversa da função dada.1. F s = 3 s 2 + 4
Em cada um dos problemas de 1 a 10, encontre a transformada de Laplace inversa da função dada.6. F s = 2 s - 3 s 2 - 4
Em cada um dos problemas de 1 a 10, encontre a transformada de Laplace inversa da função dada.4. F s = 3 s s 2 - s - 6
Em cada um dos problemas de 1 a 10, encontre a transformada de Laplace inversa da função dada.3. F s = 2 s 2 + 3 s - 4