Exercícios de Ângulo Entre Dois Vetores - Lista de Exercícios Resolvida
Questão 1
Sejam vetores tais que . Considere as afirmativas:
- e são ortogonais.
- É possível que
I e II são verdadeiras.
I é verdadeira e II é falsa
I é falsa e II é verdadeira
I e II são falsas.
Ver solução completaQuestão 2
Seja a função
Sabendo que é um produto interno em , calcule um vetor ortogonal a .
Ver solução completaQuestão 3
Consideremos, no , o produto interno usual. Para que valores de os vetores e são ortogonais?
Ver solução completa
Questão 5
Se
são matrizes quaisquer de , a seguinte fórmula define um produto interno nesse espaço:
Dados os vetores
Determinar o ângulo entre e
Ver solução completaQuestão 6
Consideremos o seguinte produto interno em , sendo e . Dados os vetores , e , calcular o cosseno do ângulo entre e .
Ver solução completaQuestão 7
Seja uma rotação em relação ao eixo . Sabe-se que . Determine o ângulo de rotação.
Dica: pense no plano perpendicular ao eixo de rotação.
Ver solução completaQuestão 8
Considere o produto interno usual do e seja um conjuto de vetores não nulos.
Assinale a alternativa VERDADEIRA:
Se não existirem dois vetores de ortogonais entre si então é linearmente dependente
Se é linearmente independente então pelo menos dois vetores de são ortogonais entre si
Se é linearmente independente então os vetores de são todos ortogonais entre si
Se é linearmente dependente então os vetores de não podem ser todos ortogonais entre si
Ver solução completaQuestão 9
Em um espaço vetorial munido de um produto interno, considere as seguintes afirmações:
Qualquer conjunto ortogonal de vetores não nulos é linearmente independentes.
Dados dois vetores não nulos e quaisquer, temos .
Qual das opções abaixo é CORRETA?
A afirmativa é verdadeira e é verdadeira.
A afirmativa é falsa e é falsa.
A afirmativa é verdadeira e é falsa.
A afirmativa é falsa e é verdadeira.
Ver solução completaQuestão 10
Para qual valor de a o triângulo é retângulo no vértice A, onde
(a) 2
(b) -4
(c) -1/2
(d) 1/4
Ver solução completaQuestão 11
O ângulo entre os vetores (1,2,2,1) e (1, 0, 2,-1) è:
(a) agudo.
(b) obtuso.
(c) reto.
(d) indefinido.
Ver solução completaQuestão 12
Sejam e e seja um vetor não-nulo e ortogonal a ambos. A transformação linear satisfaz e . Então podemos afirmar que é igual a:
Ver solução completa
Questão 13
Considere o produto interno usual do e seja um conjuto de vetores não nulos.
Assinale a alternativa VERDADEIRA:
Se não existirem dois vetores de ortogonais entre si então é linearmente dependente.
Se é linearmente independente então pelo menos dois vetores de são ortogonais entre si.
Se é linearmente independente então os vetores de são todos ortogonais entre si.
De é linearmente dependente então os vetores de não podem ser todos ortogonais entre si.
Ver solução completaQuestão 14
Considere no espaço vetorial (isto é, os polinômios de grau ) o produto interno dado por .
Assinale a alternativa VERDADEIRA:
e são ortogonais
e são ortogonais
e são ortogonais
e são ortogonais
Ver solução completaQuestão 17
Considere em os polinômios e . Em relação ao produto interno usual de , .
- Calcule .
- Calcule a distância entre e , ou seja .
- Determine o ângulo entre e .
Questão 18
Qual dos vetores abaixo forma o maior ângulo com o vetor (1,2,0,2)?
(a) (1,-3,0,2)
(b) (1,1,-3,1)
(c) (1,2,-3,3)
(d) (1,1,1,1)
Ver solução completaQuestão 19
Decida se cada afirmação abaixo é verdadeira ou falsa. Se a afirmação for verdadeira, apresente uma demonstração. Se a afirmação for falsa, exiba explicitamente um contraexemplo.
(a) Se e então e não são ortogonais seja qual for
Ver solução completaQuestão 20
No espaço dos polinômios de grau menos ou igual a 2, considere o produto interno definido como O cosseno do ângulo entra os polinômios e é:
(a)
(b)
(c)
(d)
Ver solução completaQuestão 21
Considere os vetores e de . Seja o ângulo entre eles. Então:
(a)
(b)
(c)
(d)
Ver solução completaQuestão 23
Seja um conjunto ortonormal de . Seja o tetraedro cujas arestas são representadas por . Calcule a área da superfície de :
(a)
(b)
(c)
(d)
Ver solução completaQuestão 25
Seja um espaço vetorial munido com produto interno dado por:
(a) Determine o ângulo entre os polinômios e .
Ver solução completaQuestão 26
Se em relação a uma base ortonormal , e , determine o valor de tal que seja ortogonal a e forme ângulo agudo com .
Ver solução completaQuestão 27
Considere as retas e .
- Determine a posição relativa entre e .
- Calcule o cosseno do ângulo entre e .
- Escreva uma equação vetorial para a reta que passa por e é perpendicular à . (Bônus: determine
Questão 28
No paralelepípedo da figura, , , , . Calcule o comprimento da diagonal desse paralelepípedo que tem origem em .
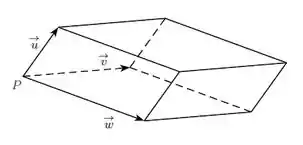
Questão 29
Em um sistema de coordenadas ortogonal são dados os pontos , e .
a) Determine as coordenadas do ponto pertencente ao segmento tal que
b) Mostre que o ângulo formado por e é igual ao ângulo formado por e .
Ver solução completaQuestão 30
Seja um conjunto de vetores dois a dois ortogonais:
– é ortogonal a
– é ortogonal a
a) Ambas são verdadeiras
b) é verdadeira e é falsa
c) é falsa e é verdadeira
d) Ambas são falsas
e) Não sei
Ver solução completaQuestão 31
Assinale o vetor que faz o menor ângulo com o vetor :
a)
b)
c)
d)
e) Não sei
Ver solução completaQuestão 32
Considere os vetores unitário e com norma 2 que formam um ângulo tal que . Calcule
a)
b)
Ver solução completaQuestão 33
Sejam e vetores do tal que e . Pode-se afirmar que, necessariamente,
- e são ortogonais
é verdadeira e é falsa
Ambas são verdadeiras
Ambas são falsas
é falsa e é verdadeira
Ver solução completaQuestão 34
Sejam e vetores ortogonais de tal que e . Qual dos vetores abaixo pode ser o vetor ?
Ver solução completa
Questão 35
Em um espaço vetorial munido de um produto interno, considere as seguintes afirmações:
Qualquer conjunto ortogonal de vetores não nulos é linearmente dependentes.
Dados dois vetores não nulos e , temos .
Qual das opções abaixo é CORRETA?
A afirmativa é verdadeira e é verdadeira.
A afirmativa é verdadeira e é falsa.
A afirmativa é falsa e é falsa.
A afirmativa é falsa e é verdadeira.
Ver solução completaQuestão 37
Considere a reta
E os pontos e Seja o ponto de tal que os ângulos e sejam congruentes. Temos que é igual a:
Ver solução completa
Questão 38
Seja o ângulo entre os vetores e Assinale a alternativa correta:
(a)
(b)
(c)
(d)
Ver solução completaQuestão 39
Sejam uma base ortonormal positiva, , , , e um ponto qualquer no espaço.
a) Sabendo que e . Mostre que , e são vértices de um triângulo.
b) Determine o ângulo . Esse é um ângulo agudo ou obtuso?
c) Mostre que .
d) Determine o vetor projeção ortogonal .
e) Determine .
f) Considere os pontos , e tais que e . Determine os valores de para que a área do triângulo seja 5.
Ver solução completaQuestão 40
Sejam e dois vetores ortogonais não nulos. Então podemos afirmar que:
Ver solução completa
Questão 41
Qual dos vetores abaixo é ortogonal ao vetor e pertence ao plano gerado pelos vetores e ?
Ver solução completa
Questão 42
Seja um conjunto ortonormal de vetores não nulos:
é verdadeira e é falsa
Ambas são verdadeiras
Ambas são falsas
é falsa e é verdadeira
Ver solução completaQuestão 43
Seja um conjunto ortonormal.
Qual das opções abaixo é a CORRETA?
e são verdadeiras.
e são falsas.
é verdadeira, mas é falsa.
é falsa, mas é verdadeira.
Ver solução completaQuestão 46
Dado o produto interno em (espaço dos polinômios da forma definido por , assinale o polinômio que é ortogonal a :
Ver solução completa
Questão 47
Seja uma rotação em torno do eixo gerado por . Suponha que mande o vetor no vetor . Calcule o ângulo da rotação. (Sugestão: Utilize a projeção no plano perpendicular ao eixo de rotação)
graus
graus
graus
graus
Ver solução completaQuestão 48
Em um sistema ortogonal de coordenadas são dados os pontos , e .
- Mostre que , e não são colineares.
- Determine as coordenadas do ponto de modo que (nessa ordem) seja um paralelogramo.
- Determine o ângulo entre e .
Questão 49
Sejam e dois vetores e sejam e . Se e e , calcule:
- O produto interno ;
- O ângulo entre os vetores e .