Exercícios de Projeção Ortogonal - Lista de Exercícios Resolvida

Sejam vetores do . Calcule a projeção ortogonal de em , utilizando a transformação projeção ortogonal, sabendo que .

Sejam um subespaço vetorial, a projeção ortogonal sobre e :

mostre que ;

mostre que o conjunto é ortogonal para todo .

Determine as matrizes das

, projeção ortogonal na reta

, projeção ortogonal sobre o plano

, projeção ortogonal na reta

, projeção ortogonal na reta

, projeção ortogonal sobre o plano

Considere, em , o cubo de aresta unitária e vértices A ,B, C, D, E, F, G, H, conforme a figura

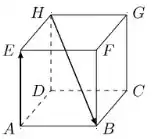
Se , então é igual a

Em , com produto interno definido por , seja , com , o polinômio de grau menor ou igual a 1 mais próximos do polinômio . Então, é igual a

Considere o subespaço e o vetor Se está munido do produto interno usual, e , com e , então é igual a

Seja um espaço vetorial qualquer munido de um produto interno e seja uma base ortonormal de com relação a esse produto interno.

1. Se e , explique como calcular sem conhecer a expressão que define esse produto interno.
2. Determine o ângulo entre e .
3. Determine a projeção ortogonal de sobre .

Calcule a distância entre o vetor e a sua reflexão ortogonal pelo plano de equação :

1. .
2. .
3. .
4. .

Considere o produto interno usual de e calcule a distância entre o ponto e a reta gerada pelo vetor

1. .
2. .
3. .
4. .

Dados os planos e , a reta e o ponto :

Sabendo que é um tetraedro e que a face tem lado com medida é um triângulo retângulo em e está contido em , a face está contida em e o vértice , determine as coordenadas dos pontos , e .

(Obs: o ponto já é conhecido).

Considere a reta e os pontos e .

a) Verifique se .

b) Determine o ponto , projeção ortogonal de sobre .

c) Determine a medida angular entre a reta que passa por e e a reta .

Seja S o plano gerado por e . A projeção ortogonal de sobre S vale:

(a)

(b)

(c)

(d)

Considere o ponto e o plano . Determine

a) A projeção ortogonal de sobre .

b) O ponto simétrico de em relação a .

Seja a matriz que representa a projeção sobre o plano ao longo da direção de (projeção ortogonal), e seja Calcule

(a)

(b)

(c)

(d)

Seja o vetor o resultado da projeção ortogonal do vetor sobre o plano Então x vale:

(a) 12

(b) 13

(c) 14

(d) 15

Considere os vetores com norma , com norma e tais que . Se e

Determine as coordenadas de na base .

Se é um pentágono regular de lado como na figura abaixo, determine

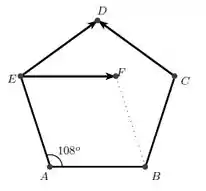
a) . (Dado: )

b) O valor de para o qual

Seja o subespaço vetorial .

a) Encontre uma base ortogonal para .

b) Determine a expressão de .

Considera o espaço dos polinômios munido do produto interno . Seja o subespaço vetorial .

a) Encontre uma base ortogonal para .

b) Encontre o polinômio de que está mais próximo de .

Considere as retas e e o plano .

a) Determine a posição relativa entre e .

b) Determine a posição relativa entre e .

c) Escreva uma equação vetorial para a reta que é a projeção ortogonal da reta sobre o plano .

Em uma base ortonormal são dados os vetores e . Determine todos os vetores que satisfazem as condições:

• é unitário.

Dados os planos e , a reta e o ponto :

Determine a projeção ortogonal do ponto sobre o plano .

Considere os vetores de

d) Determine um vetor paralelo a tal que o vetor

Seja perpendicular a .

Observe que o vetor é a projeção ortogonal de em . Aconselhamos fazer uma figura.

é uma matriz que projeta cada vetor de , ortogonalmente, sobre o plano . A segunda coluna da matriz é:

Considere o espaço vetorial munido do seu produto interno usual. Se e forem os números reais tais que é a projeção ortogonal do vetor no subespaço , então será igual a:

Escolha uma opção:

Considere os subespaços de (com usual) abaixo:

Seja o operador projeção ortogonal em . Determine .

Considere o produto interno

Definido no espaço vetorial , dos polinômios com grau menor ou igual a , e seja o subespaço de gerado por . Se , então a soma dos coeficientes de é igual a:

Escolha uma opção:

Em um base ortonormal positiva são dados os vetores , e .

1. Mostre que a sequência é .
2. Determine tal que

Seja o plano de formado pelos vetores que satisfazem .

(a) Calcule a projeção ortogonal de e de sobre .

Seja um subespaço de formado pelos vetores tais que

a) Determine a projeção ortogonal dos vetores e de sobre

Considere no espaço um triangulo ABC e sejam D e E pontos do segmento AC tais que:

Como ilustrado na figura abaixo:

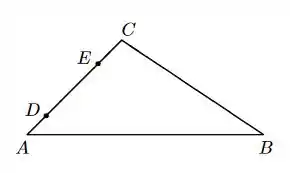
Se são tais que  e então:

1. e
2. e
3. e
4. e
5. e

Q8. Sejam   tais que e . Pode-se afirmar que:

2. O conjunto é linearmente dependente

Em , sejam planos cujas interseção é uma reta r. Sejam e vetores não-nulos de tais que e , e seja um vetor não-nulo paralelo a r. Considere as seguintes afirmações:

são paralelos

é uma base ortogonal de

é linearmente independente

Está correto o que se afirma em

Sejam , , vetores de , com tais que a medida do ângulo entre quaisquer dois vetores desses vetores seja igual a radianos. Então a projeção ortogonal de sobre é igual a

Considere o vetor o plano

E sejam tais que , em que é ortogonal a e é paralelo a . Se , então será igual a:

Considere os planos e e o ponto .

a) Escreva em equações paramétricas.

b) Determine o ângulo entre os planos e .

c) Determine a projeção ortogonal do ponto sobre o plano .

Assinale abaixo a expressão que representa a projeção ortogonal de um vetor sobre a reta gerada pelo vetor

(a)

(b)

(c)

(d)

Considere o vetor e o plano . Se com //, , então é igual a:

Considere o tetraedro regular de aresta unitária e vértices e seja M o ponto médio do lado , conforme a figura.

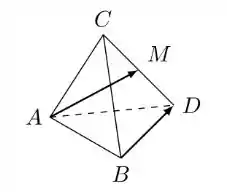
Se é tal que projeção ortogonal do vetor sobre o vetor é , então é igual a

Assinale a distância do vetor á sua reflexão ortogonal pelo plano de equação :

Considere fixada uma base ortonormal de em relação à qual são dadas coordenadas de vetores. Sejam

Seja o vetor que satisfaz as seguintes condições:

- tem norma

- é ortogonal a

-

- o ângulo entre e é agudo

Então, é igual a

a)

b)

c)

d)

e)

f)

Seja uma base ortonormal positiva. Sejam , , . Seja .

1. Ache , a projeção de sobre .
2. Calcule a área do triângulo .

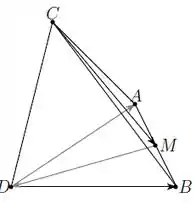
Considere um tetraedro tal que, em alguma base ortonormal , , é um ponto da aresta , e .