Um bloco de massa m = 2,0 kg encontra-se inicialmente em repouso sobre uma mesa horizontal. Os coeficientes de atrito estático e cinético entre o bloco e a mesa valem μe = 0,40 e μc = 0,20, respectivamente. Uma força F de módulo 20 N é então aplicada ao bloco, fazendo um ângulo θ com a horizontal. Considere .
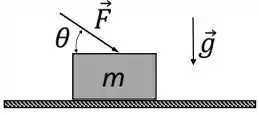
Sabendo que cos θ = 0,80 e sen θ = 0,60, a aceleração do bloco durante a aplicação da força F é:
a) 0
b) 1,6
c) 2,4
d) 4,8
e) 6,0
f) 6,8
g) 8,0
h) 9,6
i) 9,8
Passo 1
Bom, nosso primeiro passo pra uma questão de bloquinho com forças é sempre imaginar o nosso diagrama de corpo livre, né? Como a gente já sabe podemos dividir essa Força aí em duas componentes, uma no eixo x e uma no eixo y, sendo elas:
Show de bola, então no eixo x, teremos o seguinte equilíbrio de forças:
- apontando pra direita (eixo x positivo)
- apontando pra esquerda (eixo x negativo)
- apontando pra baixo (eixo y negativo)
- apontando pra cima (eixo y positivo)
Aplicamando a segunda lei de newton no eixo x, temos:
Prontinho, tá quase tudo pronto pra gente descobrir a nossa aceleração... Mas o que falta? Calcular a Força Normal!
Passo 2
Bom, como vimos no passo anterior, precisamos encontrar a força normal pra calcularmos a força de atrito. Como o bloco só se move na horizontal, vamos calcular agora o equilíbrio de forças no eixo y, então:
Show de bolinhasss!
Passo 3
Agora que já temos o valor da nossa Normal, podemos jogar ela no equilíbrio de forças no eixo x e descobrir a nossa aceleração, então voltando pro passo 1, e lembrando que se o bloco tá em movimento utilizamos o coeficiente de atrito cinético, temos:
Conseguimosss!
Resposta
d) 4,8