Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Atrito Estático + Atrito Cinético

Ver Teoria
Exercício 612345789101112131415161718192021222324252627282930313233343536373839404142434445

Enunciado

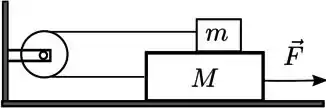
Um bloco de massa M está sob a ação de uma força horizontal F → constante sobre uma superficie horizontal sem atrito. Sobre ele há um bloco de massa m , preso à esquerda por um fio ideal. Este fio passa por uma roldana ideal que encontra-se fixa a uma parede vertical, e o conecta ao bloco de massa M . Os segmentos do fio são paralelos ao plano horizontal; vide a figura abaixo. Suponha que haja atrito entre os blocos em contato entre si. Considere como conhecidos os valores dos coeficientes de atrito estático μ e e cinético μ c , as massas M e m e o módulo da aceleração da gravidade g .

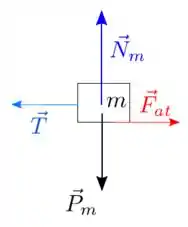
  1. Isole os blocos e represente por meio de um diagrama de corpo livre todas as forças que atuam em cada um deles.
  2. Suponha inicialmente que os blocos estejam em repouso. Determine o valor máximo do módulo de F → , F m a x para que o sistema permaneça em repouso.
  3. Considere agora que F → , cujo módulo é igual a F ' , seja capaz de colocar os blocos em movimento com aceleração constante. Para o intervalo de tempo no qual os blocos permanecem em contanto entre si, determine os vetores aceleração de cada bloco em função de F ' , μ c , m , M e g .
  4. Determine o módulo da tração do fio, para o caso do item anterior c)

Passo 1

Primeiramente vamos escrever os dados no enunciado

Dados   m M μ e μ c g

Vamos fazer isso para verificar depois cada resposta para ver se está de acordo com os dados do problema.

Passo 2

a)

Vamos responder as perguntas do passo a passo para colocar as forças, primeiro do bloco de massa M .

  1. A massa dele é considerada?

    2. Sim, ele tem massa.

  2. Ela esta encostada em alguma superfície?

    3. Sim, o bloco está apoiado no chão e no bloco de massa m .

  3. Tem algum fio?

    4. Sim, existe um fio.

  4. Tem mola?

    5. Não, não existe mola atuando.

  5. Tem atrito?

Sim, existe atrito entre os blocos

O DCL fica

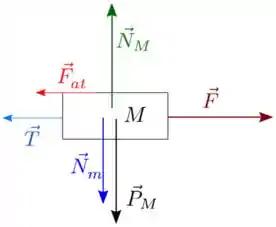
Passo 3

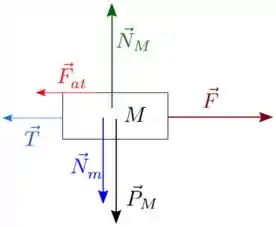
Vamos responder as perguntas do passo a passo para colocar as forças, primeiro do bloco de massa m .

  1. A massa dele é considerada?

    2. Sim, ele tem massa.

  2. Ela esta encostada em alguma superfície?

    3. Sim, o bloco está apoiado no bloco de massa M .

  3. Tem algum fio?

    4. Sim, existe um fio.

  4. Tem mola?

    5. Não, não existe mola atuando.

  5. Tem atrito?

Sim, existe atrito entre os blocos

O DCL fica

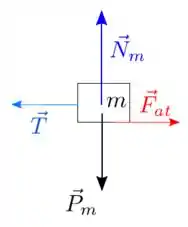
Repara que quando o bloco de baixo é puxado, para que o bloco de cima fique parado a força de atrito deve ser para a direita, porque ao puxar o bloco de baixo ele puxa o fio, que por sua vez puxa o bloco de cima para a esquerda.

A força de atrito no bloco de baixo será oposta porque o bloco de cima tende a segurar o movimento.

Passo 4

b)

O valor máximo da força vai ser quando a força de atrito estática entre os blocos for máxima. O que isso significa? Que podemos fazer

F a t = N m ⋅ μ e

Vamos fazer o equilíbrio em cada bloco.

Começando no bloco de massa m

Vamos começar pelo e i x o   y .

P m = N m

N m = m g

Passo 5

Fazendo equilíbrio no e i x o   x agora

T = F a t

T = m g μ e

Passo 6

Vamos para o equil��brio no bloco de massa M

No e i x o   y

N M = N m + P M

N M = m g + M g

N M = m + M g

Passo 7

Enquanto isso no e i x o   x

T + F a t = F m á x

T + m g μ e = F m á x

m g μ e + m g μ e = F m á x

Então

F m á x = 2 m g μ e

Passo 8

c)

Vamos reescrever os dados

Dados m M μ e μ c g F '

O DCL nesse caso fica igual a diferença é que os blocos vão se mover. O diferente dessa questão é que o bloco de massa m vai se mover para a esquerda enquanto o bloco de massa M vai se mover para a direita.

Isso faz com que

a m = - a

a M = a

Passo 9

As equações ao longo do e i x o   y não vai mudar, relembrando

N m = m g

N M = m + M g

Vamos agora para o equilíbrio ao longo do e i x o   x do bloco de massa m , tomando como sentido positivo de x forças atuanto para direita.

F R = F a t - T

Temos o caso da força de atrito dinâmica

- m a = N m μ c - T

- m a = m g μ c - T

Passo 10

Isso não resolve o problema, vamos agora para o equilíbrio da bloco M ao longo do e i x o   x

F R = F ' - T - F a t

M a = F ' - T - m g μ c

Passo 11

Temos

- m a = m g μ c - T M a = F ' - T - m g μ c

Vamos multiplicar a primeira equação por - 1

m a = - m g μ c + T M a = F ' - T - m g μ c

Somando as duas equações

m a + M a = - m g μ c + T + F ' - T - m g μ c

m + M a = - 2 m g μ c + F '

a = F ' - 2 m g μ c m + M

Passo 12

Beleza achamos o módulo da aceleração, lembra que

a m = - a

a M = a

E ambas estão na horizontal?

a → M = F ' - 2 m g μ c m + M i ^

a → m = - F ' - 2 m g μ c m + M i ^

Passo 13

d)

Das equações temos

- m a = m g μ c - T

- m F ' - 2 m g μ c m + M = m g μ c - T

Igualando os denominadores

m + M T = m 2 g μ c + M m g μ c + m F ' - 2 m 2 g μ c

m + M T = - m 2 g μ c + M m g μ c + m F '

m + M T = m F ' - m 2 g μ c + M m g μ c

T = m F ' - m 2 g μ c + M m g μ c m + M

T = m m + M F ' + g μ c M - m

Essa ultima foi meio tensa as contas hein!!

Resposta

  2. F m á x = 2 m g μ e
  3. a → M = F ' - 2 m g μ c m + M i ^

    4. a → m = - F ' - 2 m g μ c m + M i ^

  4. T = m m + M F ' + g μ c M - m

Exercícios de Livros Relacionados

Na Fig. 6-37, uma prancha de massa m 1 = 40k g repousa em um piso sem atrito e um bloco de massa m 2 = 10k g repousa sobre a prancha. O coeficiente de atrito estático entre o bloco e a prancha é 0,60
Uma curva circular em uma rodovia é projetada para uma velocidade máxima de 60k m / h . Suponha que os carros não possuem sustentação negativa. (a) Se o raio da curva é 150m , qual é o ângulo de compe
A Fig. 6-20 mostra um bloco inicialmente estacionário de massa m sobre um piso. Uma força de módulo 0,500m g é aplicada com um ângulo θ =20 ° para cima. Qual é o módulo da aceleração do bloco se (a) μ
Um ciclista se move em um círculo de 25,0m de raio com uma velocidade constante de 9,00m / s . A massa do conjunto ciclista- bicicleta é 85,0k g . Calcule o módulo (a) da força de atrito que a pista e
Sam, com 75k g de massa, dispara com seus esquis a jato descendo uma rampa de 50m verticais de altura e 10 ° de inclinação. Os esquis desenvolvem um empuxo de 200N . Na base da rampa, Sam atinge uma v