Três blocos massivos são colocadas em um sistema, conforme a figura. As massas dos blocos e valem ambas , e a massa do bloco vale . A inclinação de ambos os planos inclinados é a mesma e vale . As polias e os fios são ideais. Use para a aceleração da gravidade. Dê as respostas em termos dos dados fornecidos pelo enunciado. (Observação, quando os blocos estão se movendo, os módulos de suas respectivas acelerações possuem o mesmo valor)
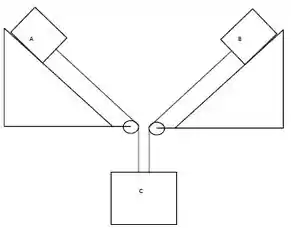
Inicialmente suponha que não há atrito entre os planos e os blocos e .
a) Faça o diagrama de corpo livre para os blocos , e .
b) Determine a aceleração do sistema.
Suponha agora que exista atrito entre os blocos A e B e os planos inclinados, e que os seus valores são idênticos.
c) Faça o diagrama de corpo livre desta nova situação.
d) Calcule o coeficiente de atrito estático mínimo entre os planos e os blocos e para os blocos permanecerem em repouso.
e) Caso os blocos já estejam se movendo, e o coeficiente de atrito cinético seja , calcule a aceleração do sistema.
Passo 1
Começamos com uma situação onde não há atrito.
Queremos o diagrama de forças sobre os três blocos.
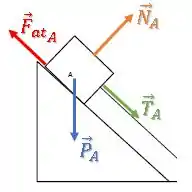
Bloco A:
Existe uma força peso para baixo, uma força normal perpendicular à superfície da rampa e uma força de tração na direção do cabo:
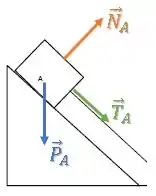
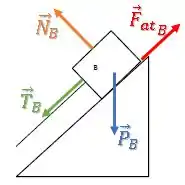
Bloco B:
Para o bloco , temos uma situação similar:
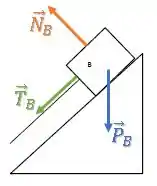
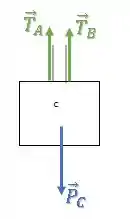
Bloco C:
Já no bloco , há uma força peso para baixo e uma força de tração em cada cabo:
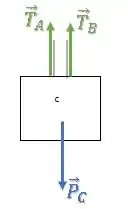
Passo 2
Na letra (b), queremos a aceleração do sistema.
Para achar a aceleração, precisamos aplicar a Segunda Lei de Newton para os blocos.
Vamos começar com o bloco :
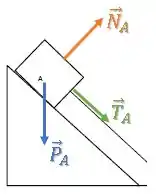
Vamos analisar a aceleração na direção paralela à rampa, então, primeiro vamos decompor essa força peso em suas componentes.
Passo 3
O ângulo de inclinação da rampa é e ele aparece bem aqui:
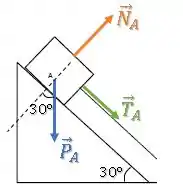
Então, suas componentes são:
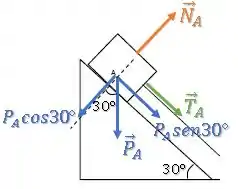
Aplicando a Segunda Lei de Newton na direção da rampa, temos:
OBS: O enunciado disse que a aceleração é a mesma para todos os blocos.
Como a situação do bloco é exatamente a mesma (massa, inclinação, forças), são simétricos, sua equação resultante da Segunda Lei de Newton vai dar a mesma do bloco :
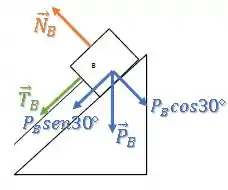
Passo 4
Agora, vamos aplicar a Segunda Lei de Newton para o bloco :
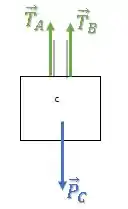
Substituindo as expressões para as forças de tração, temos:
A força peso é dada pela massa vezes a gravidade. Além disso, a massa do bloco é :
Cortando a massa :
O seno de é conhecido e vale , então:
Passo 5
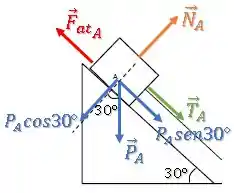
Na letra (c), agora vamos considerar que existe atrito. Queremos os novos diagramas de forças.
Bom, a força de atrito vai atuar contra a tendência de deslizamento dos blocos.
Assim, se os blocos tendem a deslizar para baixo da rampa, a força de atrito atua no sentido para cima da rampa.
Bloco A:
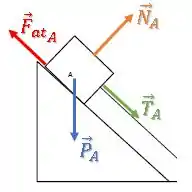
Bloco B:
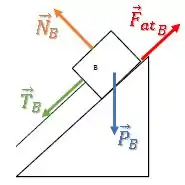
Bloco C:
Já o diagrama do bloco fica idêntico:
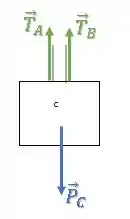
Passo 6
Na letra (d), queremos saber qual o coeficiente de atrito estático que permita o nosso sistema ficar em equilíbrio.
Então, vamos aplicar a segunda lei de Newton para a nova configuração.
Porém, dessa vez, vamos começar pelo bloco .
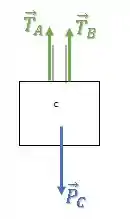
Como o corpo está em equilíbrio, a força resultante é nula:
Mas, como o problema é simétrico e o próprio enunciado diz que os blocos e sofrem a mesma força de atrito, as forças de tração nos cabos serão iguais:
Então, temos que:
Passo 7
Agora, vamos ao aplicar a segunda lei para o bloco :
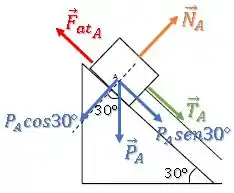
Como o corpo está em equilíbrio, a força resultante é nula:
Se queremos o mínimo coeficiente de atrito estático capaz de manter em equilíbrio o sistema, isso significa que a força de atrito estático está em seu valor m��ximo e qualquer peteleco é capaz de fazer o bloco deslizar.
A força de atrito estático máxima é dada por:
Mas quem é essa força normal ?
Passo 8
Podemos achar essa força normal fazendo o equilíbrio de forças na direção perpendicular à rampa:
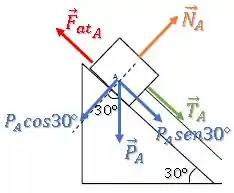
Então, a força de atrito máxima será dada por:
Passo 9
Aplicando essa força de atrito no equilíbrio de forças, temos:
Podemos cortar e ficamos com:
Substituindo os valores de seno e cosseno de :
Passo 10
Na letra (e), ele muda novamente as condições.
Agora, o sistema já está se movimentando e o coeficiente de atrito cinético é:
Queremos a nova aceleração.
Vamos, novamente aplicar a Segunda Lei de Newton, considerando agora uma aceleração:
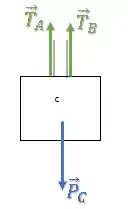
Novamente, pela simetria do problema, as forças de tração serão iguais:
Passo 11
Voltando para o bloco , temos:
A força normal terá o mesmo valor que calculamos fazendo o equilíbrio na direção perpendicular à rampa:
Substituindo isso, temos:
Cortando a massa :
Aplicando os valores numéricos de e seno e cosseno de :
Essa será a aceleração do sistema para a força de atrito cinética.
Resposta
(a)
Bloco :
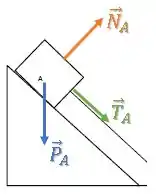
Bloco :
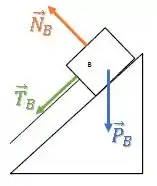
Bloco :
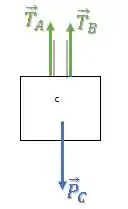
(b)
(c)
Bloco A:
Bloco B:
Bloco C:
(d)
(e)