USP, Sem Campus, Física 1, Coletânea de Exercícios - Parte I - Cinemática, Leis de Newton, Trabalho e e Energia, Questão 44b
Os esquemas de corpos e polias na figura mostram sistemas constituídos por blocos de massas e e roldanas ideais, uma fixa e a outra móvel, pelas quais passam fios inextensíveis. As massas das roldanas e dos fios são desprezíveis comparadas às dos blocos. O bloco está apoiado em uma mesa e os coeficientes de atrito entre eles valem e . Para cada um dos esquemas, determine:
A aceleração da massa quando:
Figura e ;
Figura e ;
Passo 1
Oiie, tudo bem com você?
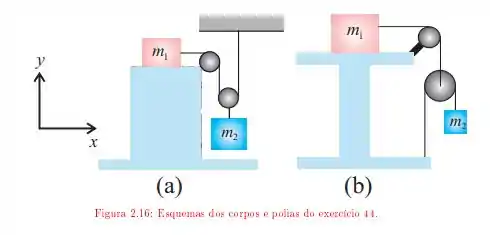
O enunciado nos apresenta duas montagens diferentes utilizando polias e cordas, da seguinte forma
Temos que entre o bloco de massa está preso ao bloco de massa , arbitrárias, através de um sistema de cordas e polias. Existe também atrito entre o bloco e a superfície em que está em contato com coeficientes estáticos e cinéticos dado por e . Tendo ambas as montagens precisamos encontrar para ambos os casos
A aceleração da massa quando:
Figura e ;
Figura e ;
O segredo é obter a aceleração através da segunda lei de Newton
Na última alternativa montamos equações para o movimento vertical e horizontal de cada bloco em cada caso! Vamos fazer isso novamente!
Passo 2
Começando com a situação , temos que as componentes horizontais e verticais das forças nos dão duas equações da forma
e
usando que
temos que
e
Vamos analisar agora o outro corpo!
Passo 3
Para o outro corpo temos apenas a relação
note que coloquei o sinal negativo na aceleração pois estou considerando que o movimento do bloco dois é para baixo, se minha escolha estiver errada, encontraremos negativo no final! Subtraindo a equação obtida para o primeiro corpo, temos que
e, portanto, obtemos
substituindo os valores dados, temos que
ou seja, temos a relação
Vamos continuar analisando o sistema!
Passo 4
A relação entre as acelerações em ambos os casos é bastante conhecida! Note que devido a polia móvel o corpo se move com o dobro da aceleração do corpo , temos que
e, portanto, obtemos que
ou seja, temos que
e, portanto, temos que
Isso foi o primeiro caso! Vamos analisar o segundo!
Passo 5
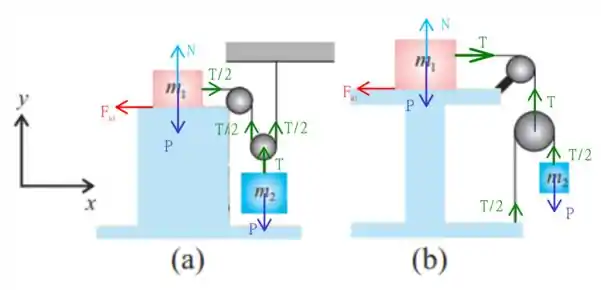
Podemos analisar o segundo caso analogamente! Mas, como está indicado no diagrama de forças do passo , a distribuição das forças muda um pouco! Temos que para o primeiro corpo as equações são
e
e, para o segundo corpo
multiplicando a equação do segundo corpo por , temos que
O sistema é bastante parecido com o que fizemos antes! Vamos agora eliminar a tensão da jogada!
Passo 6
Subtraindo os dois resultados que obtivemos, temos que
usando as massas dadas, cuidado que agora elas invertem em relação ao caso contrário! Temos que e , portanto
ou seja, novamente temos a relação
Agora, como temos uma montagem levemente diferente, o corpo se move com uma aceleração duas vezes maior que o corpo , ou seja, temos que
de forma que iremos obter as mesmas acelerações, mas trocadas, sendo elas
e
Essa alternativa foi! Vamos para a próxima agora!
Resposta