Um bloco de massa igual a 10 kg é empurrado continuamente contra uma parede vertical por uma força horizontal de intensidade igual 100 N, como mostrado na primeira figura. O coeficiente de atrito estático entre o bloco e a parede é igual a 0,60 e o coeficiente de atrito cinético é igual a 0,40. O bloco está inicialmente em repouso. Tanto no item (a) quanto no item (b) , faça um diagrama de corpo livre do bloco e use g=10 m/ .
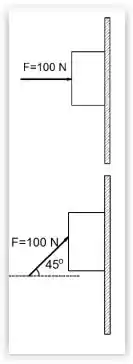
(a) (1,0 ponto) O que acontece com o bloco? Justifique a resposta.
(b) (1,0 ponto) Se a mesma força de 100N for aplicada com inclinação para cima de 45° em relação à horizontal, como mostra a segunda figura, o que acontece com o bloco? Justifique a resposta.
Passo 1
Como pedido, vamos começar fazendo o diagrama de corpo livre do bloco da figura de cima.
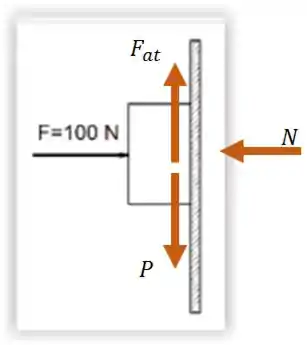
Temos:
A força peso para baixo.
A força normal perpendicular à superfície em que o bloco se apoia.
A força de atrito contrária ao sentido aparente do movimento.
A força F, que é a força que empurra o bloco contra a parede.
Passo 2
Agora vamos analisar o que acontecerá com o bloco. Para isso, vamos fazer a equação das forças nos eixos vertical e horizontal.
No eixo horizontal, temos uma aceleração igual a zero. Assim, podemos montar:
Além disso, sabemos que a força de atrito máxima é dada por:
Como a massa é de 10 kg, o peso valerá:
Montando a equação vertical, vemos que a força peso é maior do que a força de atrito máxima, logo o bloco tenderá a descer, escorregando para baixo.
Passo 3
Vamos analisar agora o segundo desenho no qual a força é aplicada com uma inclinação de 45°. Começando pelo diagrama de corpo livre:
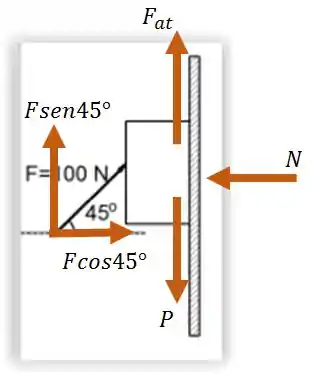
Temos:
A força peso para baixo.
A força normal perpendicular à superfície em que o bloco se apoia.
A força de atrito contrária ao sentido aparente do movimento.
A força F pode ser decomposta em duas forças: e
Passo 4
Já sabemos que para sabermos o que acontece com o bloco precisamos entender o módulo das forças que atuam nele.
Se a resultante entre a componente da força F e a força peso for menor que a força de atrito, o bloco deslizará. Caso contrário, ficará em repouso.
Vamos então analisar as equações na horizontal e na vertical.
Na horizontal a aceleração é zero, logo:
Agora vamos analisar a equação vertical. Para isso vamos utilizar a relação da força de atrito estática máxima com a normal e com o coeficiente de atrito:
Na vertical, temos então que:
Escolhendo o sentido para cima como positivo, montamos:
Logo, o bloco ficará em repouso.
Resposta
- O bloco escorregará para baixo.
- O bloco ficará em repouso.