Força de Atrito
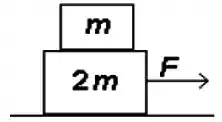
Uma pequena caixa de massa é colocada em cima de uma caixa maior de massa como mostrado na figura. Quando uma força é aplicada na caixa grande, ambas as caixas se movem para a direita com a mesma aceleração. Supondo que o coeficiente de atrito entre todas as superfícies é , qual é a força atuando na massa menor?
a)
b)
c)
d)
e)
Passo 1
Nomeando o bloco menor como bloco 1 e o bloco maior como bloco 2.
Primeiramente vamos aplicar a segunda lei de Newton no sistema como um todo:
Substituindo a formula da força de atrito:
Agora aplicando a segunda lei de Newton apenas ao bloco menor, podemos encontrar a força resultante que age sobre ele:
Substituindo a aceleração que descobrimos:
Resposta
Letra
Exercícios de Livros Relacionados
Na Fig. 6-37, uma prancha de massa m 1 = 40k g repousa em um piso sem atrito e um bloco de massa m 2 = 10k g repousa sobre a prancha. O coeficiente de atrito estático entre o bloco e a prancha é 0,60
Uma curva circular em uma rodovia é projetada para uma velocidade máxima de 60k m / h . Suponha que os carros não possuem sustentação negativa. (a) Se o raio da curva é 150m , qual é o ângulo de compe
A Fig. 6-20 mostra um bloco inicialmente estacionário de massa m sobre um piso. Uma força de módulo 0,500m g é aplicada com um ângulo θ =20 ° para cima. Qual é o módulo da aceleração do bloco se (a) μ
Um ciclista se move em um círculo de 25,0m de raio com uma velocidade constante de 9,00m / s . A massa do conjunto ciclista- bicicleta é 85,0k g . Calcule o módulo (a) da força de atrito que a pista e
Sam, com 75k g de massa, dispara com seus esquis a jato descendo uma rampa de 50m verticais de altura e 10 ° de inclinação. Os esquis desenvolvem um empuxo de 200N . Na base da rampa, Sam atinge uma v