Os esquemas de corpos e polias na figura mostram sistemas constituídos por blocos de massas e e roldanas ideais, uma fixa e a outra móvel, pelas quais passam fios inextensíveis. As massas das roldanas e dos fios são desprezíveis comparadas às dos blocos. O bloco está apoiado em uma mesa e os coeficientes de atrito entre eles valem e . Para cada um dos esquemas, determine:
O vetor força que a haste, que suporta a roldana fixa, exerce sobre a mesa, em termos dos versores cartesianos e .
Passo 1
Oiie, tudo bem com você?
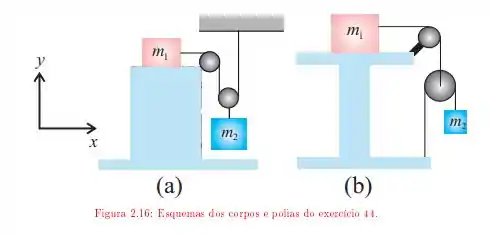
O enunciado nos apresenta duas montagens diferentes utilizando polias e cordas, da seguinte forma
Temos que entre o bloco de massa está preso ao bloco de massa , arbitrárias, através de um sistema de cordas e polias. Existe também atrito entre o bloco e a superfície em que está em contato com coeficientes estáticos e cinéticos dado por e . Tendo ambas as montagens precisamos encontrar para ambos os casos
O vetor força que a haste, que suporta a roldana fixa, exerce sobre a mesa, em termos dos versores cartesianos e .
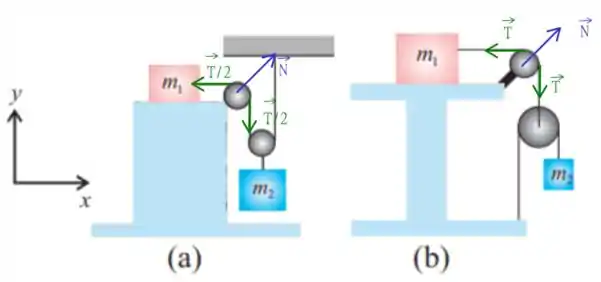
Note que o esquema apresentado já traz o diagrama de forças para cada uma das polias! Como a polia não se move a força resultante sobre ela deve ser nula, já que estamos em equilíbrio, sendo assim, vamos encontrar uma força normal (para cada caso) tal que
Em adição vamos usar as equações que obtivemos analisando o movimento dos corpos e as acelerações obtidas na alternativa anterior
Para encontrar explicitamente a força que a roldana faz sobre a mesa! Vamos lá!
Passo 2
Para o primeiro caso, temos que a dinâmica é regida por
horizontalmente, temos
e, verticalmente
ou seja, a força normal é uma força cujos componentes são dados por
Vamos achar explicitamente estes componentes! Saca só!
Passo 3
Do segundo corpo obtemos a relação
Portanto, temos que
Sendo assim, a força normal é
A força normal é a força que a superfície exerce sobre a polia, agora, a força que a polia exerce sobre a mesa é obtida usando a terceira lei de Newton como
Vamos fazer isso para o segundo caso agora!
Passo 4
O processo para o segundo caso é bastante similar, o diagrama de forças agora nos leva a uma força normal da forma
e, usando a equação para o segundo corpo no segundo caso, temos que
usando a aceleração obtida para o segundo caso e a nova massa, temos que
E, portanto, a força normal é
e, assim como anteriormente, pela terceira lei de Newton, temos que
A segunda montagem requer mais da estrutura física do que a primeira montagem! A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta