Um corpo de massa escorrega sobre um plano horizontal com coeficiente de atrito cinético e estático , como na figura. Um conjunto de polia e corda sem massa e sem atrito liga este corpo a outro corpo de massa , pendurado na vertical.
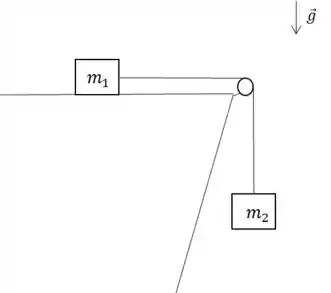
a) Calcule a aceleração do sistema.
b) Calcule a nova aceleração do sistema se colocamos um corpo de massa firmemente preso sobre o corpo 1.
c) Para a situação do item , qual deveria ser a massa mínima de modo que e se movessem em qualquer situação?
Passo 1
Vamos desenhar as forças que estão agindo sobre os corpos no sistema:
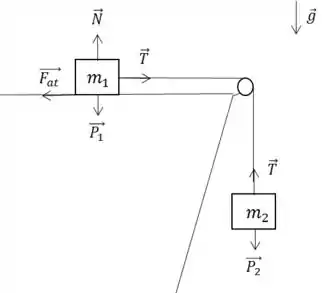
Aplicando a segunda lei de Newton para o bloco . Sabemos que no eixo não tem aceleração, então:
Aplicando no eixo :
Aplicando a segunda lei de Newton para o bloco :
Agora temos duas equações para fazer um sistema:
Somando as duas equações:
Substituindo os dados temos que:
Agora precisamos saber se a força de atrito é estática ou cinética. Vamos calcular a força de atrito estática máxima.
Como a , ou seja, é menor que a força que impulsiona o bloco. Então o bloco está em movimento, e a força de atrito é na verdade a força de atrito cinética. Logo, voltando a nossa equação:
Passo 2
b)
Nesse caso vamos ter exatamente o mesmo sistema, chegando à equação:
Calculando a força de atrito estática máxima:
Como , ou seja, é maior que a força que impulsiona os blocos e . Então o sistema vai ficar no regime estático, prevalecendo a força de atrito estática. Dessa forma, a aceleração do sistema é nula.
Passo 3
c)
Para que o sistema entre no regime cinético, temos que:
No item anterior calculamos essa força de atrito:
Resposta
a)
b)
c)