Um bloco de massa é mantido em repouso, pressionado contra uma parede vertical por uma força de módulo , conforme mostra a figura. Sabendo que os coeficientes de atrito estático e cinético entre o bloco e a parede são, respectivamente, e , o que pode-se afirmar sobre o módulo da força de atrito entre a parede e o bloco?
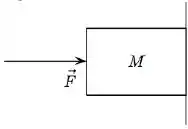
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
Passo 1
Como o bloco está sendo mantido em repouso, não há deslizamento. Assim, a força de atrito que está atuando sobre ele é estática.
Passo 2
Vamos desenhar o diagrama de corpo livre do bloco.
A força já está desenhada.
Temos a força peso apontando para baixo e a força normal perpendicular à superfície de contato (parede).
Além disso, a tendência de deslizamento do bloco é para baixo, então, a força de atrito atua contra essa tendência de deslizamento (para cima):
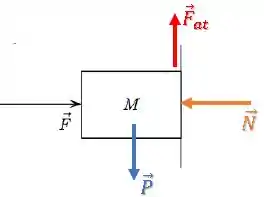
Passo 3
Okay, vamos ao módulo da força de atrito .
Temos que prestar atenção nessa parte!

Apenas a força de atrito estática máxima que pode ser calculada com a expressão:
Ou seja, apenas quando o corpo está na iminência de deslizar que podemos usar essa expressão para a força de atrito.
Antes de atingir seu valor máximo, a força de atrito apresenta um valor suficiente para impedir o deslizamento.
Como assim?
Se aplicamos uma força num corpo, tentando movê-lo, a força de atrito vai atuar na direção contrária a esse deslizamento e com o mesmo módulo da força que aplicamos.
Dessa forma o corpo consegue ficar em equilíbrio e não deslizar!
Passo 4
Para descobrir a força de atrito nesse caso, basta aplicar a segunda lei de Newton:
Como o bloco está em repouso, temos:
Olhando na direção vertical, ficamos com:
Ou seja, a força de atrito está sendo responsável por equilibrar a força peso e não deixar o bloco cair.
Ficamos com a alternativa (e).
Resposta
Letra (e)