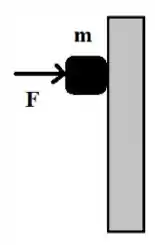
a) Na figura acima, um bloco de massa é empurrado contra uma parede por uma força horizontal de módulo . O coeficiente de atrito estático entre a parede e o bloco é 0,35. Verifique, através de cálculos explícitos, se nestas condições o bloco fica em repouso ou cai deslizando pela parede.

Seja agora a situação apresentada na figura abaixo, consistindo de dois blocos de massas (bloco menor) e (bloco maior). Uma força horizontal de módulo é aplicada ao bloco menor. O coeficiente de atrito estático entre os blocos é 0,40 e o de atrito cinético é 0,35. O coeficiente de atrito estático entre o bloco e o solo é 0,30 e o coeficiente de atrito cinético é 0,25.

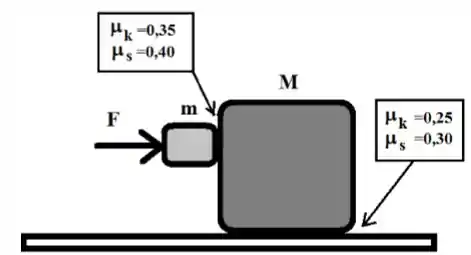
b) Nesta situação, o conjunto dos dois blocos se movimenta na horizontal? Justifique sua resposta através de cálculos explícitos.

c) Calcule a força de atrito entre os dois blocos, argumentando, com cálculos, se esta força é estática ou cinética.

(b)

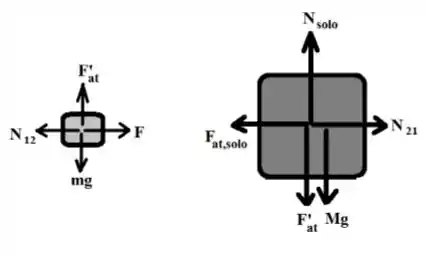
Supondo que o sistema não se movimenta na horizontal, a força que se compensa ao atrito do solo é a própria força aplicada (analisando o conjunto como um todo). Nesta hipótese, temos pra a 2a Lei de Newton: Na vertical:

Na horizontal:

é a força de atrito entre os dois blocos e vai depender se o bloco menor esta escorregando ou não. Como estamos supondo que o sistema esta inicialmente parado na horizontal, podemos observar que e então a força máxima de atrito estática entre os blocos será

Como o peso do bloco menor é:

E este valor é menor que o valor máximo do atrito estático entre os blocos, então o bloco menor fica parado e . Assim:

Assim:

Como então o sistema se movimenta na horizontal.

(c)

Como os dois blocos estão em movimento, então (conclusão do item ). Temos que calcular o valor de (para depois comparar o peso do bloco menor com o valor da força máxima de atrito estático entre os blocos) A 2ª lei de Newton fica neste caso (veja diagrama de forças):

Bloco menor:

Bloco maior:

Horizontal:

Vertical:

Fazendo temos:

Como os blocos estão em movimento.

Daí de , e , temos em função de .

Temos duas opções para : ou ela é igual a (bloco menor não cai) ou ela é cinética e menor que (bloco cai). Supondo que não caia:

e de obtemos:

Com este valor de tem-se:

Força Máxima de atrito estático entre blocos

Como o peso do bloco menor é que é MENOR que a força de atrito estática máxima entre os blocos, então a suposição de que é estática é correta. Assim, o bloco menor está parado em relação à parede do bloco maior. [Se supusermos que inicialmente o bloco menor está se movendo, calculamos através de cinética e chegaremos a uma inconsistência.]

CONCLUSÃO: a força de atrito entre os blocos é ESTÁTICA e seu valor é o peso do bloco menor, .