Uma caixa de está em repouso sobre uma superfície horizontal. Os coeficientes de atrito estático e cinético entre o par de superfícies são respectivamente e . Uma força horizontal de é aplicada sobre a caixa. A força de atrito exercida pela superfície sobre a caixa é:
(A)
(B)
(C)
(D)
(E)
Passo 1
Uma caixa está em repouso sobre uma superfície horizontal.
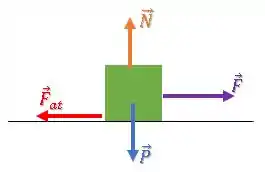
Logo, há uma força peso e uma força normal que se cancelam na vertical:
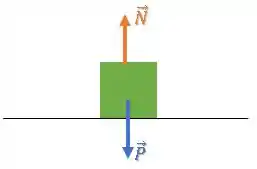
Aí, uma força horizontal é aplicada na caixa:
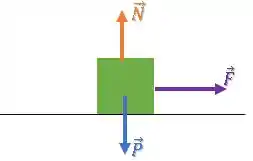
Mas existe uma força de atrito que vai agir contra a tendência de deslizamento da caixa, ou seja para a esquerda:
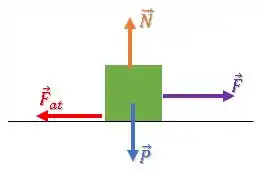
Nós queremos descobrir o valor dessa força de atrito .
Mas qual é a dúvida?
Lembra que a força de atrito estática tem um valor máximo dado por:
Se a força puxando a caixa ultrapassar esse valor, a caixa entra em movimento e a força de atrito estática vira uma força de atrito cinética, calculado com o outro coeficiente de atrito ():
Porém, se a força puxando a caixa não ultrapassar o valor de , a caixa permanece em repouso, pois a força de atrito é capaz de anular a força .
Então, basta saber se a força ultrapassa ou não a força de atrito estático máxima. Para saber qual tipo de atrito está atuando sobre a caixa.
Passo 2
A força de atrito estática máxima será:
Podemos obter essa força normal a partir do equilíbrio na vertical.
Passo 3
Fazendo o equilíbrio de forças na vertical, temos:
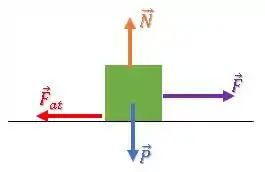
Substituindo os valores:
Assim, a força de atrito máxima será:
Portanto, como a força é de apenas , ela não é capaz de ultrapassar o limite máximo do atrito estático e fazer a caixa entrar em movimento.
Passo 4
Assim, a caixa estará em repouso e por isso também há um equilíbrio de forças na horizontal:
Ficamos com a letra (D).
Resposta
Letra (D)