UFRJ – Física 1 – P1 – 2019.2 – Discursiva
Um bloco de massa se encontra sobre a superfície de um plano inclinado de ângulo . Um bloco , de massa , colocado em cima do bloco , está unido por um fio ideal a um pino fixo, como mostra a figura.
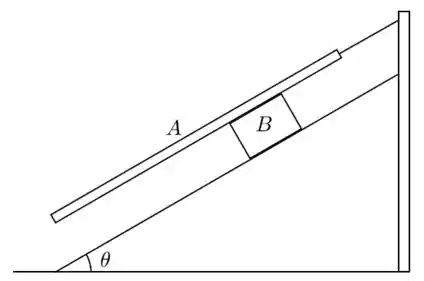
Ao liberar o bloco ele desliza sobre o plano, mantendo contato com o bloco . Se o coeficiente de atrito cinético entre todas as superfícies em contato é :
- Faça o diagrama das forças para cada bloco.
- Calcule a tração no fio.
- Determine a aceleração de descida do bloco .
Expresse os resultados em termos de , , e .
Passo 1
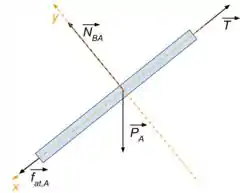
Se liga! Vamos fazer o diagrama de forças para o bloco .
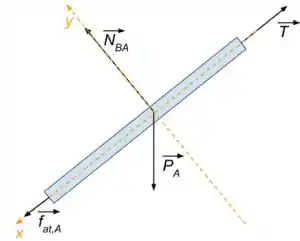
Onde temos que é a tração no fio que segura o bloco, é o peso do bloco, é a reação normal do bloco em e é a força de atrito entre os blocos A e B.
Passo 2
Ainda no item (a), precisamos fazer o diagrama de forças para o bloco . Veja como fica na figura abaixo.
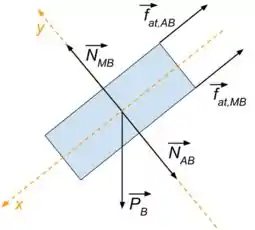
Onde temos é o peso do bloco, é a reação normal do bloco em , é a reação normal do plano sobre o bloco B, é a força de atrito entre os blocos e , é a força de atrito entre a plano e o bloco .
Pronto, finalizamos o item (a). Agora podemos partir para o item (b).
Passo 3
No item (b), ele pede a Tração no fio.
Sabendo que o bloco permanece, temos que
Podemos verificar, usando a geometria que
Portanto
Lembra que ?
No nosso caso a normal que queremos é .
Vamos achala-la usando as forças em .
Portanto
Substituindo na eq (1), temos
Passo 4
Agora precisamos resolver o item (c). Levando em consideração que o bloco só se movimenta no eixo
Novamente aplicando a geometria, temos
Sabendo que e é um par ação e reação, temos
Logo
Para o eixo , temos
Temos que as forças e é um par ação e reação, logo
Sabendo que
Temos
Agora só precisamos melhorar a nossa expressão e isolar .
Resposta
