USP, Sem Campus, Física 1, Coletânea de Exercícios - Parte I - Cinemática, Leis de Newton, Trabalho e e Energia, Questão 43a
No esquema mostrado na figura , o carrinho de massa pode deslizar sem atrito, enquanto os coeficientes de atrito entre e a superfície horizontal valem e e .
Qual deve ser o menor valor de para que se inicie o movimento?
Passo 1
Eaew, tudo certinho com você?
O enunciado descreve a situação representada por
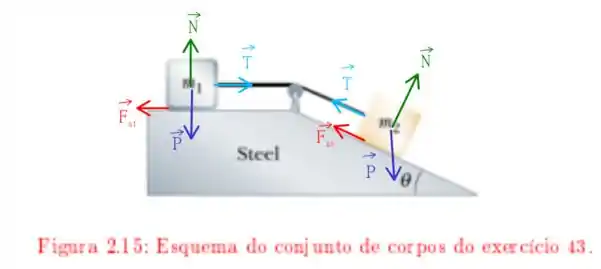
em que temos duas massas e inicialmente arbitrárias. Temos que a rampa está livre de atrito, mas a parte horizontal tem os seguintes coeficientes de atrito estático e cinético . O ângulo de inclinação é , tendo todas estas informações em mente queremos encontrar
Qual deve ser o menor valor de para que se inicie o movimento?
Temos que analisar a situação em que todas as forças acima fogem do equilíbrio, como queremos a massa mínima , vamos procurar a condição de equilíbrio!
Vem comigo!
Passo 2
As forças atuando sobre o corpo de massa como
que nos dá as equações
e
em que usei
Analogamente, para o segundo corpo, temos que
e
note que estou diferenciando os referenciais e , em que o segundo é um referencial inclinado devido ao plano! No entanto, para obter os módulos desejados, isso não será importante! Note que a inclinação já é considerada quando escrevemos os componentes das forças! Eu igualei todas as expressões a pois procuramos uma situação de equilíbrio! Vamos calcular a nossa massa!
Passo 3
Da segunda equação em temos que
da primeira equação em , temos que
ou seja, temos que
Vamos aplicar este resultado nas equações em !
Passo 4
Da segunda equação em temos que
como temos que
ou seja, temos que
Usando o valor de calculado no passo anterior, temos que
ou seja, a massa de equilíbrio é tal que
usando os valores no enunciado, temos que
Ou seja, precisamos que a massa seja vezes maior que a massa ! A primeira alternativa foi isso! Vamos para a próxima!