A figura a seguir mostra o bloco () conectado a uma parede rígida por uma corda ideal, repousando sobre o bloco (). O bloco está submetido a uma força horizontal para a direita que pode variar em módulo. Adote .
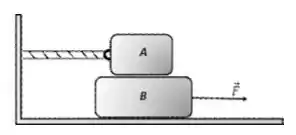
O sistema repousa sobre um solo que oferece atrito desprezível. Só existe atrito na superfície entre os blocos (). A situação inicial é de repouso.
a) Faça o diagrama de corpo livre para cada um dos blocos isoladamente. Não calcule valores, apenas nomeie todas as forças que agem em cada bloco.
b) Para o caso em que , e supondo que a corda não se rompe, calcule os vetores força de todas as outras forças que agem sobre os blocos. Use o sistema de coordenadas padrão: eixo positivo apontando para a direita, eixo positivo apontando para cima. (Dica: calcule primeiro o valor da fora de atrito estático máximo entre os blocos.)
c) Para o caso em que , calcule os módulos da aceleração do bloco e da força de tração da corda sobre o bloco , supondo que a corda não se rompe.
d) Suponha agora que a corda não exista, mas que todos os outros dados do enunciado principal sejam repetidos. Calcule o valor máximo que a força pode assumir de tal modo que não haja deslizamento relativo entre os blocos, ou seja, eles aceleram juntos.
Passo 1
a)
Essa parte é simples, basta não se esquecer das forças de ação e reação de contato (normal e atrito).
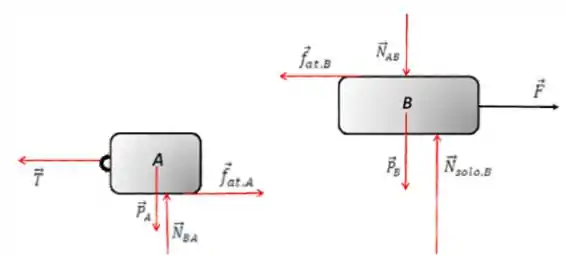
Passo 2
b)
Vamos seguir a dica do enunciado e calcular primeiramente o valor da força de atrito máxima entre os blocos. Para isso, temos que primeiro encontrar o valor da força normal.
Aplicando a segunda lei de Newton para as forças sobre o bloco , no eixo , sabendo que :
Agora sim, vamos calcular o valor máximo da força de atrito estática entre os blocos:
Como a força é menor que a força de atrito estática máxima, o sistema se manterá em repouso. Sendo assim, o módulo da força de atrito será igual ao de .
Calculando as demais forças, temos as forças sobre o bloco no eixo , sabendo que :
E também as forças sobre o bloco no eixo , sabendo que :
Finalmente, as forças sobre o bloco no eixo , sabendo que :
Passo 3
c)
Agora, como o módulo de supera o atrito estático máximo, o bloco sairá do repouso (o bloco não, pois a corda não se rompe). Como há deslizamento entre as superfícies dos blocos, o atrito passa a ser cinético e de valor:
Assim, para o bloco , teremos, no eixo , sabendo que :
Para o bloco , teremos, no eixo :
Passo 4
d)
Na situação limite de não deslizamento relativo entre os blocos, o atrito entre eles atingirá o valor estático máximo , e essa força de atrito será a própria resultante horizontal agindo sobre o bloco :
Como o bloco move-se junto com o bloco , podemos considerar o sistema composto pelos dois blocos como um único corpo rígido, de massa total igual a , com a aceleração calculada de . Como a força é a única a atuar na horizontal sobre o sistema composto, ela é a própria resultante horizontal:
Resposta
a)
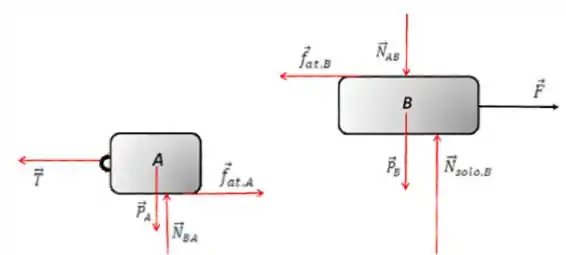
b)
c)
d)